Week 5

Geospatial Visualization

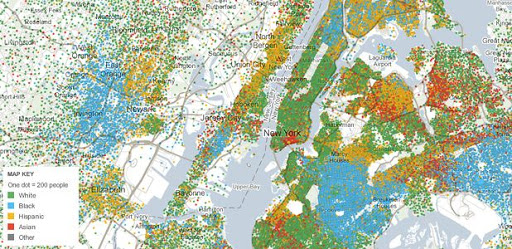
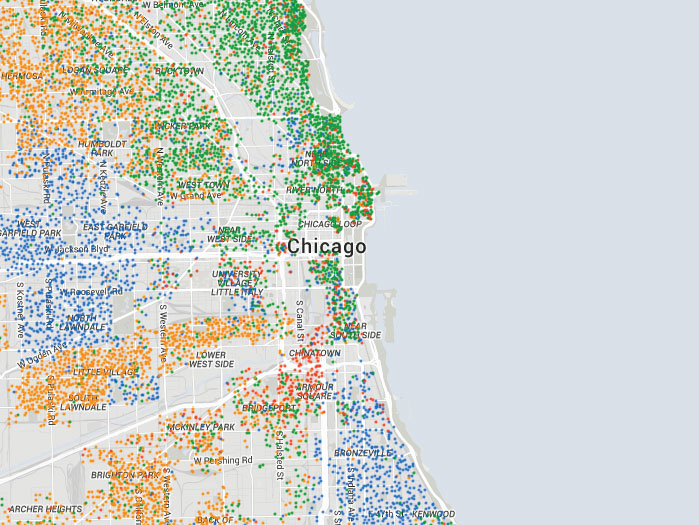
What can we say about the people in an area - you can enter a zip code to explore an area using their tool.
https://www.esri.com/en-us/arcgis/products/tapestry-segmentation/zip-lookup

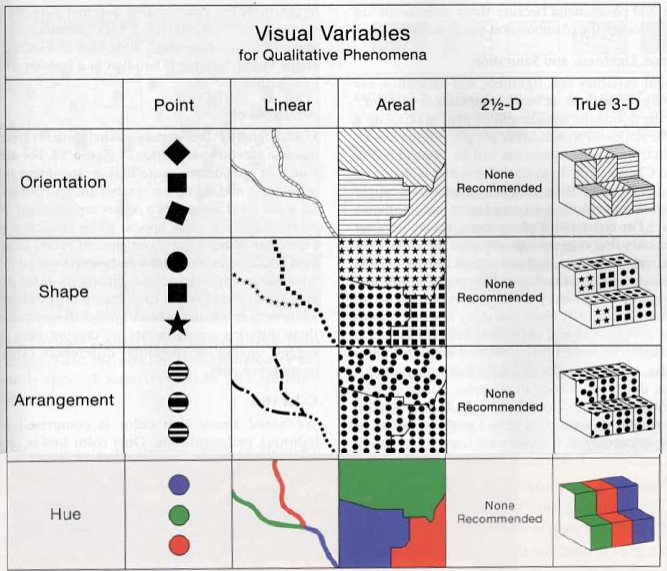
Visual contrasts established by manipulating perceptual qualities

the following are retinal variables - perceived immediately and effortlessly - fundamental units of visual communication

• Size
• Value (saturation)
• Orientation
• Texture
• Shape
• Position
• Hue

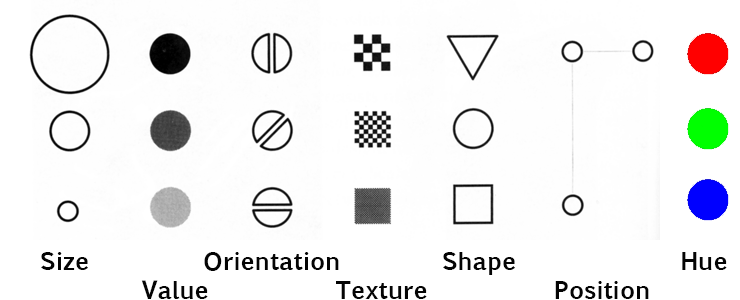
Information represented in a visual display is characterized by

• Number of dimensions (things being measured)
• Length of each dimension (number of possible values in each dimension)
• Scale of measurement for each dimension
  • nominal (categorical) (associative, selective) - distinct categories should be obvious (e.g. representations of census data on religion, or martial status or hair color or whether you call a carbonated soft drink pop / soda / coke)
    
  • ordered - determine relative ordering - which one is 'more' than the other should be obvious (e.g. representations of questionnaire answers with low, medium, high options)
    
  • quantitative - determine amount of difference between ordered values - how much 'more' should be obvious (e.g. representations of census data on age in years or income in dollars)

Lets do an example. For each of the two projects below write what you think the length and scale are for each dimension in a word processing file. Print the file and add it to your gradescope submission for the week. Note that for many data visualization tasks the data will constantly be increasing as more is collected, so its important not only to think of the values currently in the dataset, but the values that are likely to be in the dataset as it grows.

The data from Project 1 in 2020, which can be found at https://www.evl.uic.edu/aej/424/litterati challenge-65.csv , included the following 11 dimensions. Take a few minutes and decide on the length and scale of each of these dimensions.

• id (system id of the person picking up and tagging pieces of rubbish)
• email address (email address of the person picking up and tagging pieces of rubbish)
• latitude (of the piece of rubbish that was picked up)
• longitude (of the piece of rubbish that was picked up) time
• tags (for type of rubbish that was picked up)
• url (for the photo of the piece of rubbish that was picked up)
• username (user name of the person picking up and tagging pieces of rubbish)
• country_code
  

The data from Project 1 in 2019, available at https://aqs.epa.gov/aqsweb/airdata/annual_aqi_by_county_2019.zip , included the following 19 dimensions. Take a few minutes and decide on the length and scale of each of these dimensions.

• State (US State)
• County (US County)
• Year
• Days with AQI (days with air quality data)
• Good Days (number of 'good' days that year)
• Moderate Days
  
• Unhealthy for Sensitive Groups Days
• Unhealthy Days
• Very Unhealthy Days
• Hazardous Days
• Max AQI (max air quality index score that year)
• 90th Percentile AQI
• Median AQI
• Days CO (number of days with carbon monoxide measurements)
• Days NO2
• Days Ozone
• Days SO2
• Days PM2.5
• Days PM10
  

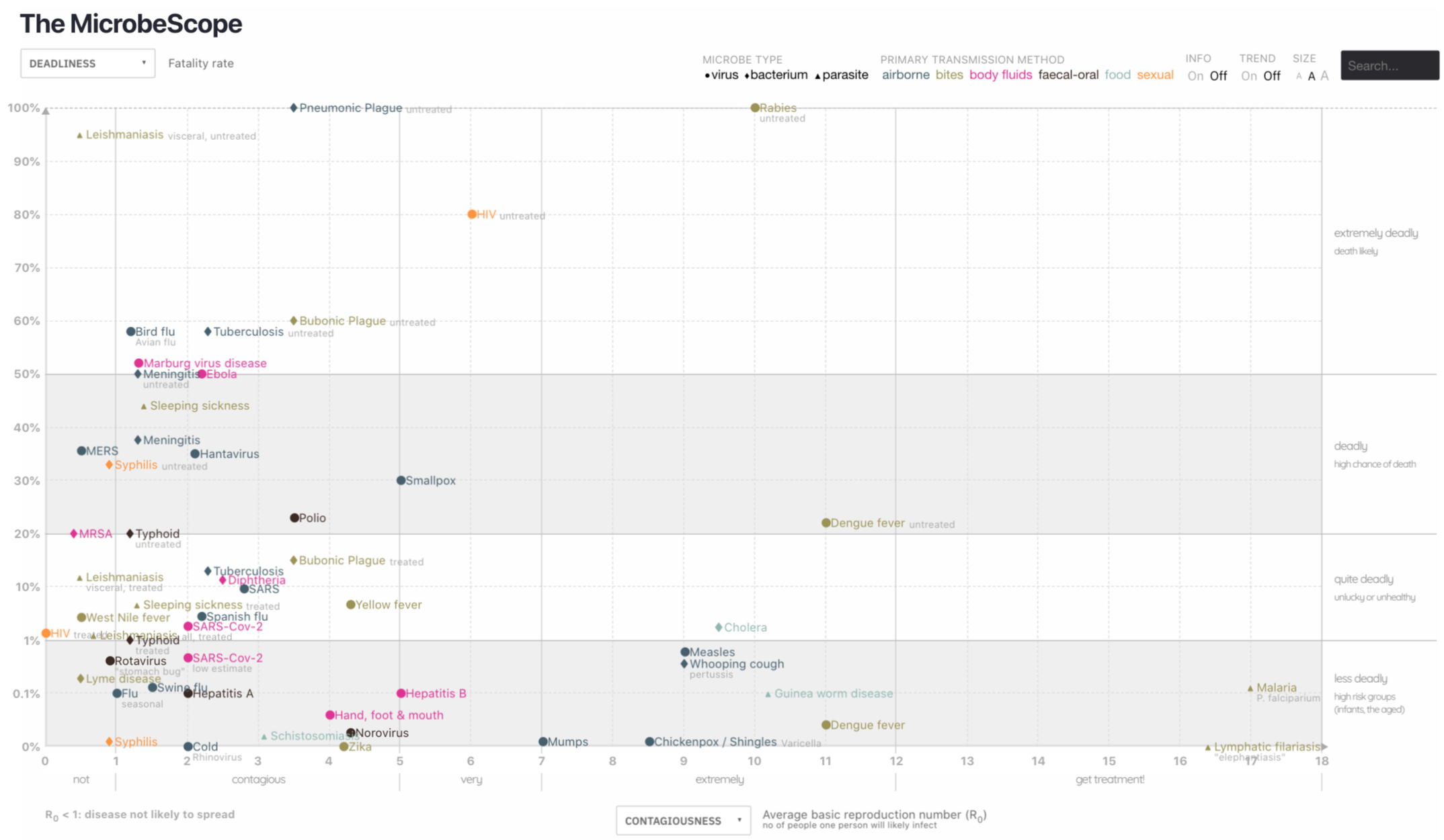
We can look back at the MicrobeScope example. Here all of the points have the same Size, but there are different Shapes (circles, diamonds, triangles) and different Hues (dark blue, light blue, pink, etc.) and they are in different Positions in the
chart.

Here microbe type (shape) and primary transmission method (hue) are nominal / categorical.
Deadliness, Contagiousness, and the other X and Y axis options are quantitative

Nominal - User interested in categorizing

In associative perception the viewer ignores variation in one visible dimension in reading the remainder of the display

An associative variable does not affect the visibility of other dimensions (e.g. we can recognize hue regardless of orientation.) A variable is dissociative if visibility is significantly reduced for some values along that dimension (e.g. its hard to determine hue of a very thin line or small dot)

Orientation, Texture, Shape, Position, Hue are associative

Size and Value are dissociative - they dominate perception and disrupt processing of other correlated dimensions
 

In selective perception viewer attempts to isolate all instances of a given category and perceptually group them into a single image. The task is to ignore everything but the target value on the dimension of interest - to see at a glance where all the targets are within the display
  

All the variables except shape are selective - it can be vary hard to pick out different shapes, as we saw with the yes / no table.


  

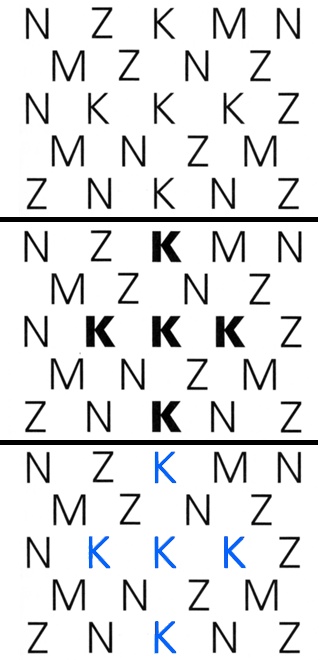
In ordered perception the viewer must determine the relative ordering of values along a perceptual dimension. Given any two visual elements, a natural ordering must be clearly apparent so the element representing 'more' of the corresponding quality is immediately obvious

Size, Value, and Position are ordered

In quantitative perception the viewer must determine the amount of difference between two ordered values. The user does not need to refer to an index or key - the relative magnitudes must be immediately apparent

Size and Position are quantitative

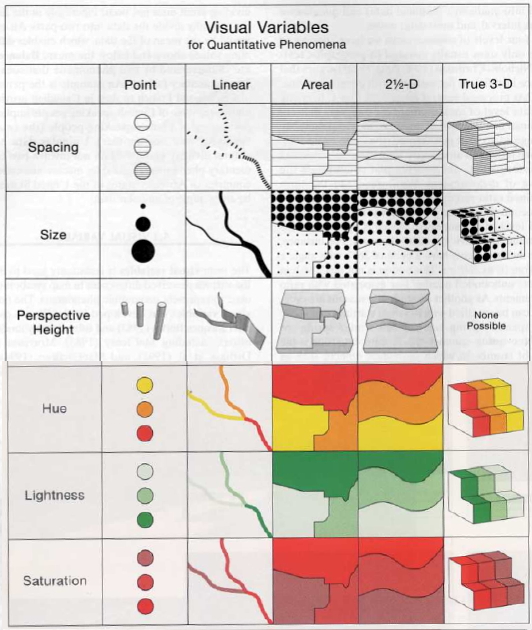
Visual variables differ substantially in length:

• Shape is longest - almost infinite variety, but can be hard to tell apart if they are too similar
  
• Position in 2D space is limited by display size and resolution, but very fine grained
• Size and Hue 10-15
• Value and Texture support less than 10
• Orientation is shortest - confusion arises if more than 4 levels are attempted

The Principles of Symbolization chapter from Thematic Cartography and Geovisualization, 3rd ed. by Slocum, McMaster, Kessler, and Howard gives a nice introduction on mapping data to symbols so we will use several examples from it below.

Nature of Geographic Phenomena:

Spatial Dimension

• 0d - point phenomena located in 2d or 3d space (e.g. data collected at weather monitoring stations)
• 1d - linear phenomena (e.g. the path an AUV or a drone takes while taking measurements)
• 2d - areal phenomena (e.g. data collected on the surface of a lake)
• 2.5d - volumetric phenomena - each x, y position has a single z value associated with it (e.g. the maximum depth at any point in the lake)
• 3d - volumetric phenomena - each x, y, z position has a value associated with it (e.g. the ph values collected at various points and depths in the lake)

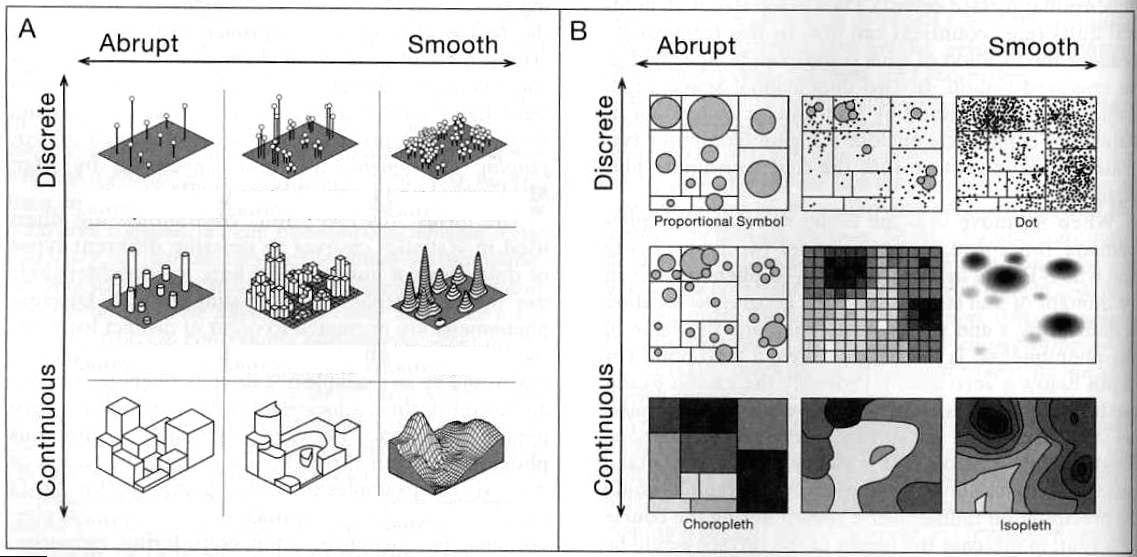
Type of visualization used depends both on the nature of the underlying phenomenon and the purpose of the map

• We previously looked at a variety of weather maps where the data was collected from a set of discrete weather stations but formed a very smooth continuous map.
• We looked at  the pop / soda / coke map where the data was collected from discrete individuals but formed a less smooth and less continuous map.
• We looked at the map for gas prices where the data was collected from discrete locations, but which showed abrupt changes on political boundaries.
  
• We looked at the map of target stores opening that had very discrete points.
  

We often deal with continuous data represented by discrete sampling

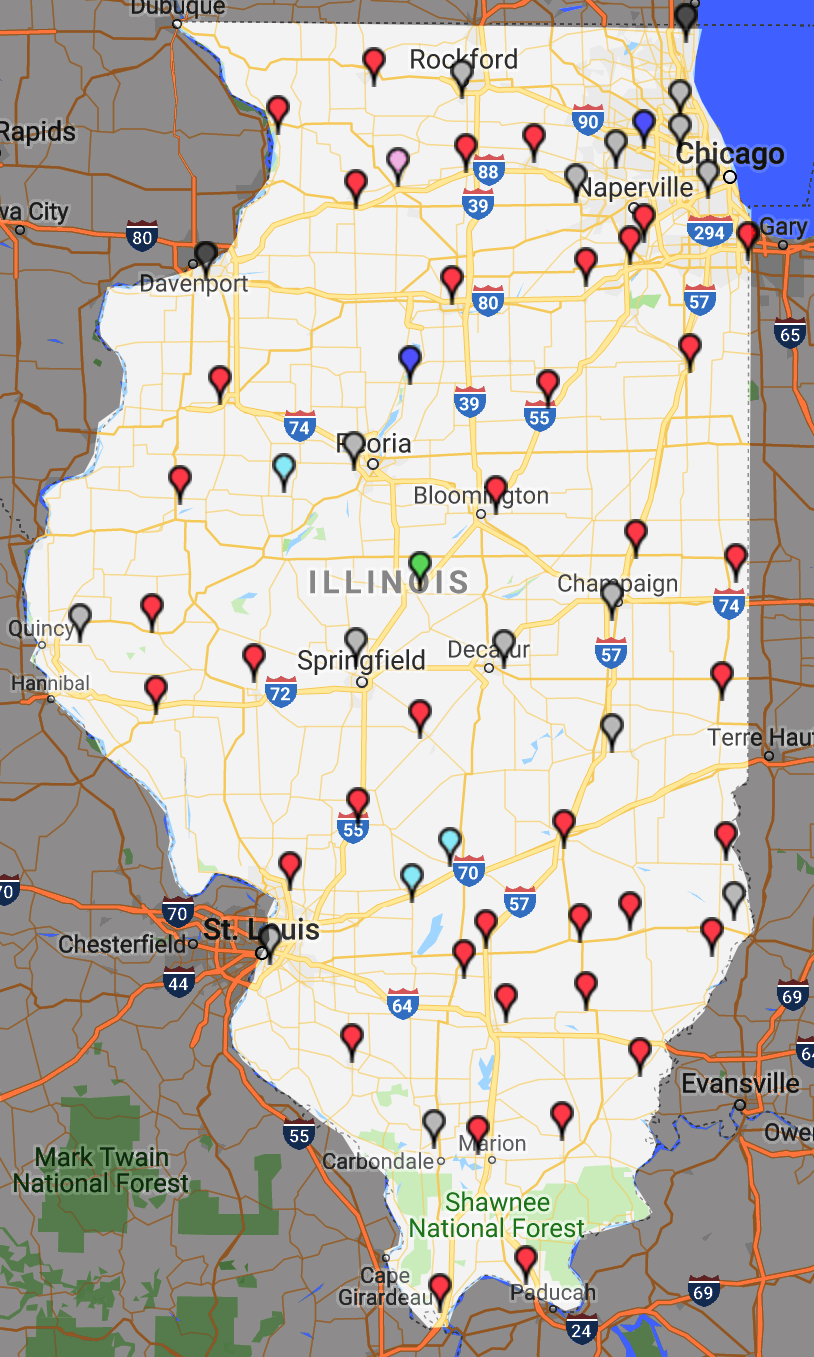
A familiar example is a weather map showing the current temperature across the state or country, but the data is only sampled at certain scattered stations which is then interpolated. You can click on the map to gain access to the data files and to see how the data is interpolated across the state. Here are the FAA sites in Illinois https://www.faa.gov/air_traffic/weather/asos/?state=IL

Interpolation is then used to predict the values in between, with a variety of possible methods.

• (nearest neighbor)
• linear
• quadratic
• etc
  

shepards method is one way to perform that interpolation - https://en.wikipedia.org/wiki/Inverse_distance_weighting

Air quality data usually changes slowly but if you live in Hawaii near a volcano or live in an area prone to forest fires, the values may change much faster and may regularly impact your life, so dashboards that show the value now and predict it into the future, like we typically predict rain on maps, can be very useful.

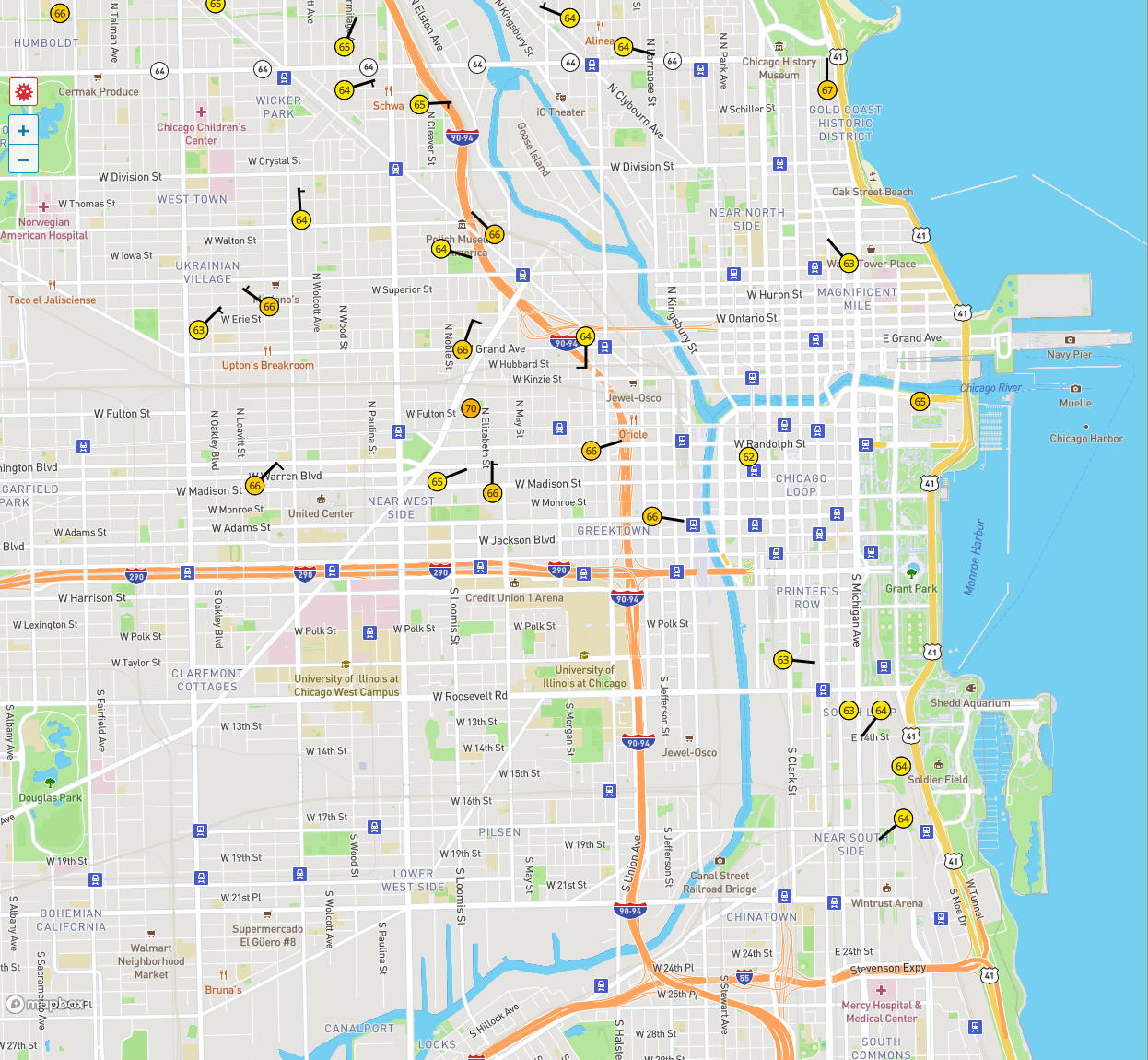
This map is nice as you can see the values for the individual stations and the contours generated from that data, which also helps to see how the contours are generated from the individual data locations.

https://gispub.epa.gov/airnow/

• orientation - direction/orientation of the marks/symbol
  
• shape - different shapes are used
  
• arrangement - different arrangement of marks making up the symbol
  
• hue - different colors are used but careful choices need to be made here so there is NO sense of 'less' to 'more' in the different hues

• spacing (texture) - smaller spacing between marks suggest higher value
• size - larger symbol or larger marks making up the symbol suggests a higher value
  
  
• perspective height - higher elevation suggests a higher value (cant be used for 3D phenomena because all 3 dimensions are already in use)
  
  
• color (hue) - what is the dominant wavelength (red, green, blue, etc but careful choices need to be made here so there IS a sense of 'less' to 'more' in the progression on hues) 
  
• color (lightness) - how light or dark the color is (light green, dark green)
• color (saturation) - how far is the intensity is from grey (bright red, muted red)

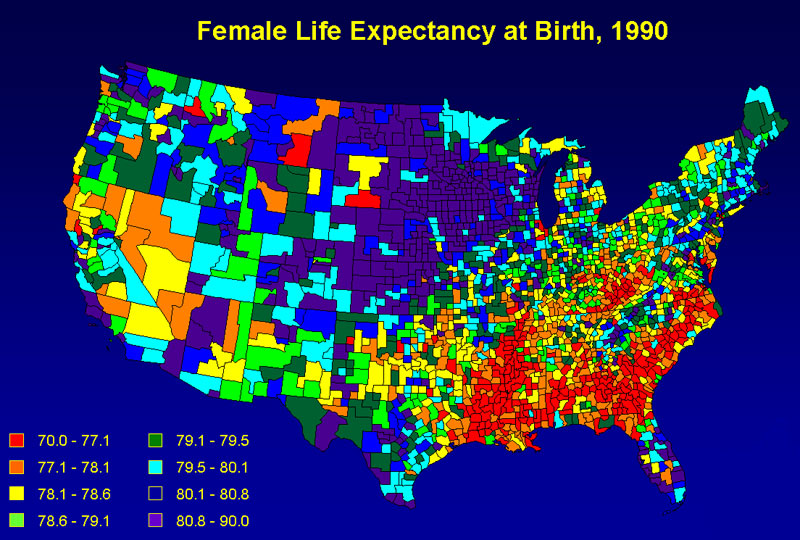
here is an example of different ways of using colour to map life expectancy in the US which is quantitative. Which is more readable? the first from mapoftheunitedstates.org or the second from www.measureofamerica.org

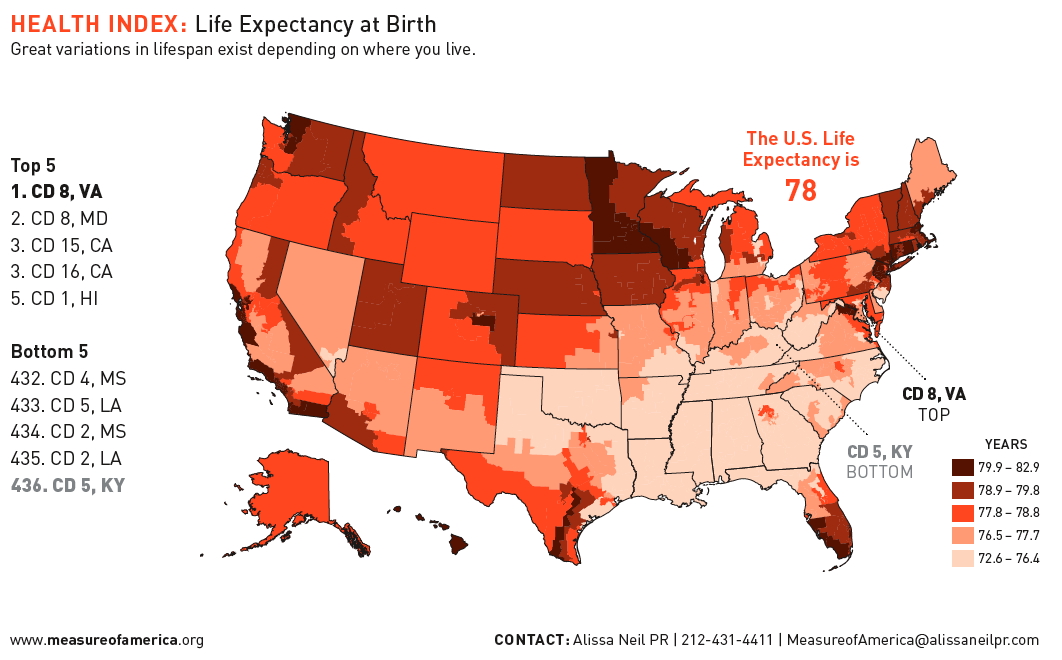So, lets try an in class activity to make this more clear, and for that we will take a look at mapping the data for the winning countries of the Eurovision Song Contest from 1956 to the present - https://en.wikipedia.org/wiki/Eurovision_Song_Contest

Here are the totals:

and there is a current map of Europe available here:

You can use a computer/tablet to create a visualization with the map, or print out the map and use colored pencils, or some other visualization primitives and then take a photo of the map, convert it to pdf and add it to your gradescope submission for the week.

Comparison of choropleth, proportional symbol, isopleth, and dot mapping:

choropleth commonly used to portray data collected for units such as counties or states regions are shaded / colored based on the phenomena good for when values change abruptly at unit boundaries but hides variation within units, and the boundaries may be artificial in relation to the phenomena. isopleth (contour map) good when data collected was from a smooth continuous phenomenon regions are shaded / colored based on the phenomena interpolating set of isolines between sample points of known values proportional symbol scale symbols in proportion to the magnitude of the data symbol might be a true point (located at a data collection point) or a conceptual point (at the center of a unit) dot mapping one dot is set equal to a certain amount of the phenomenon dots should be placed where the phenomena occurs (much higher level of accuracy than other maps)

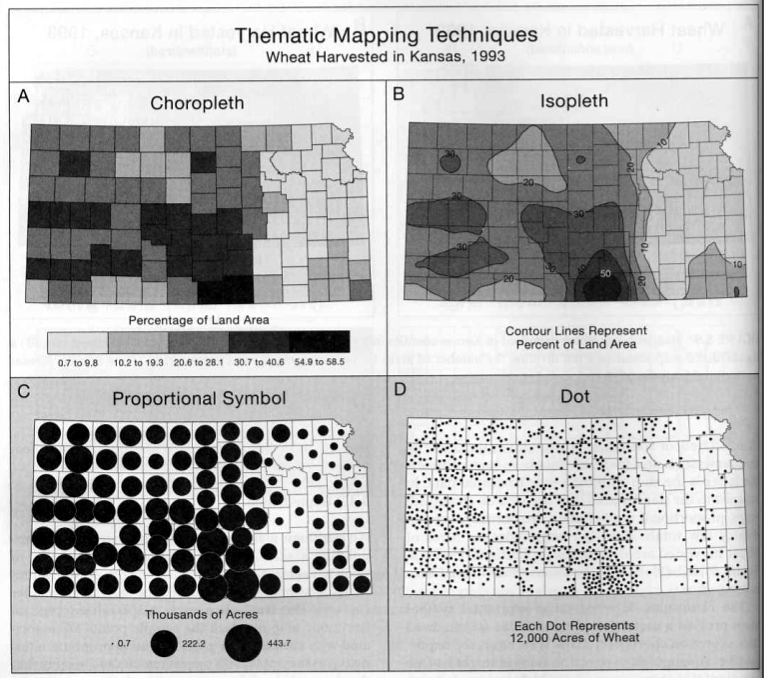Figure 5.10 from Thematic Cartography

R has variety of nice libraries and available data to help with this kind of thing. The following code reads in data on counties in the US as well as a file of data to map onto those counties (in this case number of electric vehicles, population, and number of passenger cars registered in each Illinois county). Since the county names match in both files its pretty simple to join them together and then display the results as a couple different choropleth maps.

Create a new Jupyter notebook for this activity and when you are done print out that notebook and add it to your gradescope submission for the week.

conda install -c conda-forge r-ggmap
conda install -c conda-forge r-mapdata
conda install -c conda-forge r-ggthemes
conda install -c conda-forge r-sp

usually these commands have worked for me, but I have found that if I have loaded in some other odd packages into anaconda that conda hits some incompatibilities and has a hard time dealing with them. In those cases I have found it simpler to start over with a new R environment (the notes from week 2) and then install the packages above.

#
# example of mapping data onto Illinois counties
# based on example from https://people.ohio.edu/ruhil/Rbook/maps-in-r.html

library(ggplot2)
library(ggmap)
library(maps)
library(mapdata)
library(ggthemes)
library(sp)
library(stringr)
library(plyr)

usa <- map_data("county")
il <- subset(usa, region == "illinois")

il$county = str_to_title(il$subregion)

#basic map with county boundaries and county names at the centroid of the county
getLabelPoint <- # Returns a county-named list of label points
    function(county) {Polygon(county[c('long', 'lat')])@labpt}
centroids = by(il, il$county, getLabelPoint)     # Returns list
centroids2 <- do.call("rbind.data.frame", centroids)  # Convert to Data Frame
centroids2$county = rownames(centroids)
names(centroids2) <- c('clong', 'clat', "county")

#simple map with county borders and county names
ggplot() + geom_polygon(data = il, aes(x = long, y = lat, group = group), fill = "white", color = "gray") + coord_fixed(1.2)  + geom_text(data = centroids2, aes(x = clong, y = clat, label = county), color = "darkblue", size = 2.25)  + theme_map()

# read in data on the number of electric vehicles registered in each county
evs <- read.table(file="http://www.evl.uic.edu/aej/424/EVs_in_IL_2021.csv", sep=",", header=TRUE)

# under windows the first column header gets corrupted - this fixes it
names(evs)[1] <- 'county'

# as usual here you should take a look at the data and see if the numbers make sense

#combine the county data and the EV data - they have the 'county' attribute in common
# join keeps the original ordering where merge does not
ilCountyPlusEV <- join(il, evs)

#plot the population per county
ggplot() + geom_polygon(data = ilCountyPlusEV, aes(x = long, y = lat, group = group, fill = population), color = "black") + coord_fixed(1.2) +
    geom_text(data = centroids2, aes(x = clong, y = clat, label = county), color = "black", size = 2.25) + scale_fill_distiller(palette = "Oranges", direction=1) +
    labs(fill = "population") + theme_map()

#plot the percentage of cars to people in each county
ggplot() + geom_polygon(data = ilCountyPlusEV, aes(x = long, y = lat, group = group, fill = percent_cars), color = "black") + coord_fixed(1.2) +
    geom_text(data = centroids2, aes(x = clong, y = clat, label = county), color = "black", size = 2.25) + scale_fill_distiller(palette = "Oranges", direction=1) +
    labs(fill = "car %") + theme_map()

#plot the total number of EVs per county
ggplot() + geom_polygon(data = ilCountyPlusEV, aes(x = long, y = lat, group = group, fill = evs), color = "black") + coord_fixed(1.2) +
    geom_text(data = centroids2, aes(x = clong, y = clat, label = county), color = "black", size = 2.25) + scale_fill_distiller(palette = "Oranges", direction=1) +
    labs(fill = "# of EVs") + theme_map()

#plot the percentage of cars that are EVs in the county and reverse the scale
ggplot() + geom_polygon(data = ilCountyPlusEV, aes(x = long, y = lat, group = group, fill = percent_cars_evs), color = "black") + coord_fixed(1.2) +
    geom_text(data = centroids2, aes(x = clong, y = clat, label = county), color = "black", size = 2.25) + scale_fill_distiller(palette = "Oranges", direction=1) +
    labs(fill = "EV %") + theme_map()

#There are better (more complicated) ways to use color here
#details at https://ggplot2.tidyverse.org/reference/scale_brewer.html
#but this should give you a starting point for what you can do

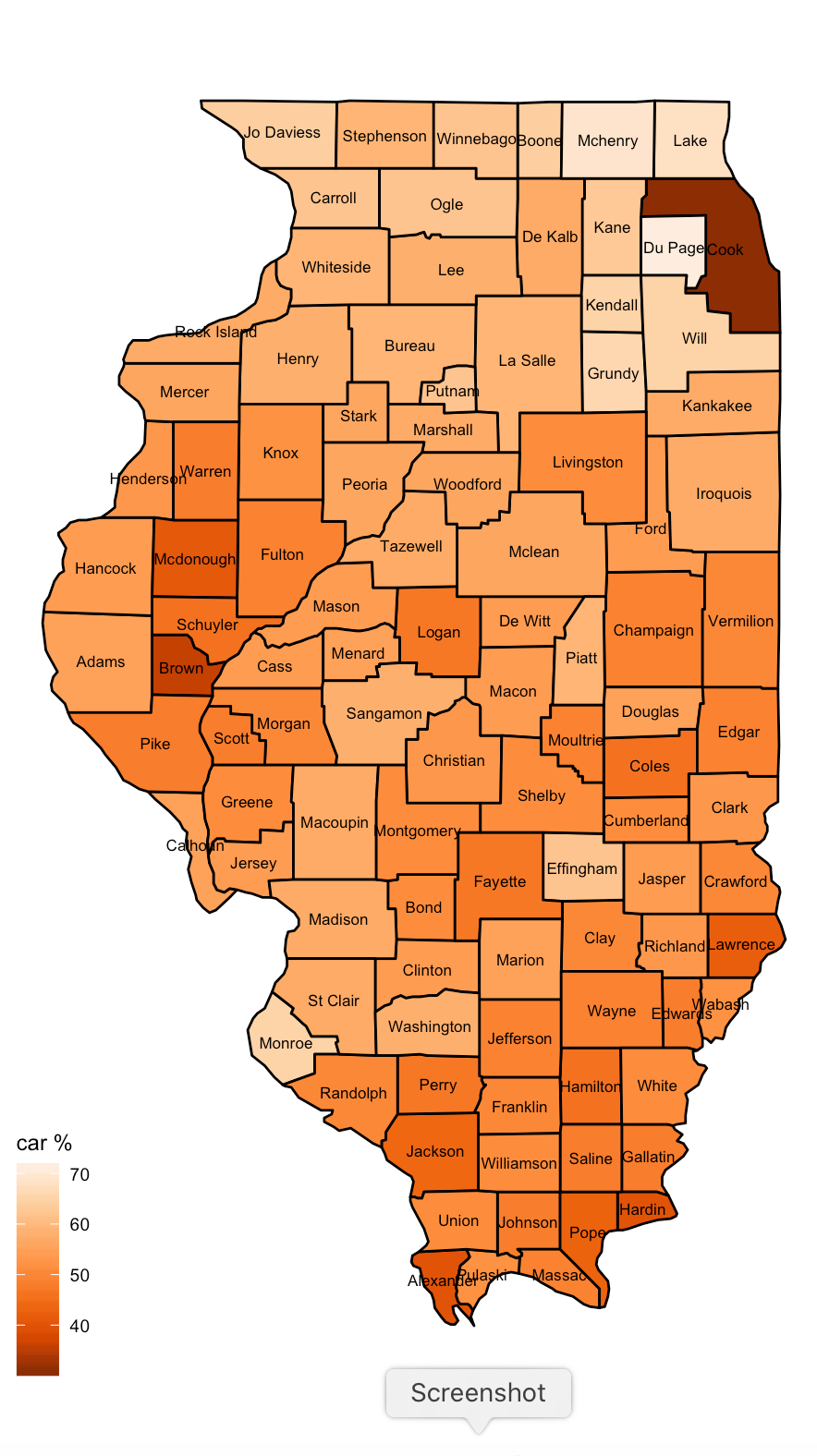
after this, try and show the counties in a different US State or show another set of countries as in this web page https://www.datanovia.com/en/blog/how-to-create-a-map-using-ggplot2/

this makes it really easy to map data onto filled county / state / country regions, though as we saw above, choropleth maps are not always the most intuitive representation.

There are also pictographic symbols

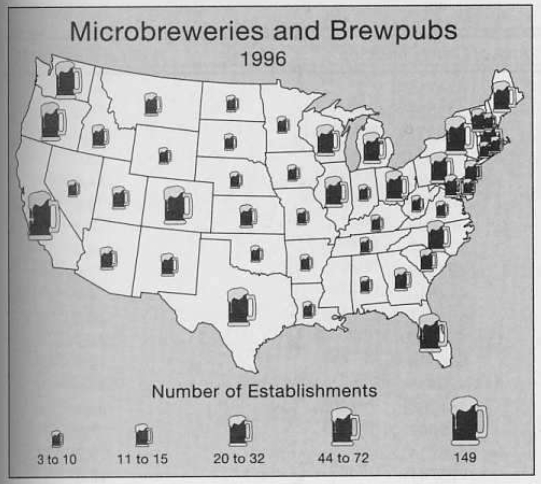
Here is an image showing crime statistics compared to the average over time for the US from CommonGIS via the Thematic Cartography and Geovisualization book showing why this can be tricky ...

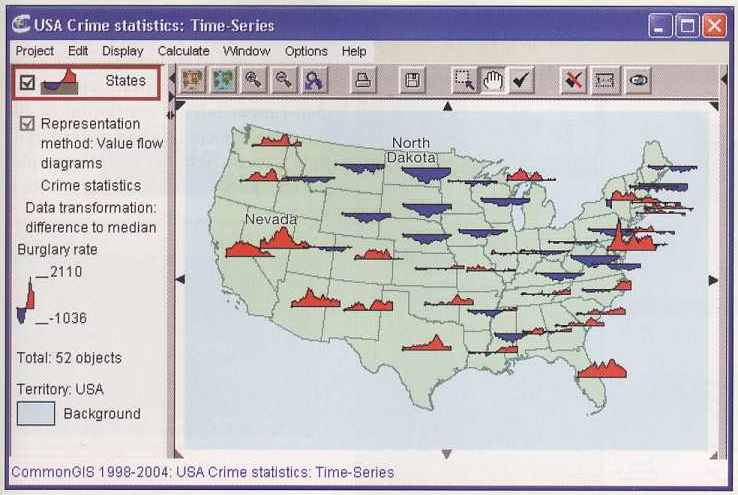
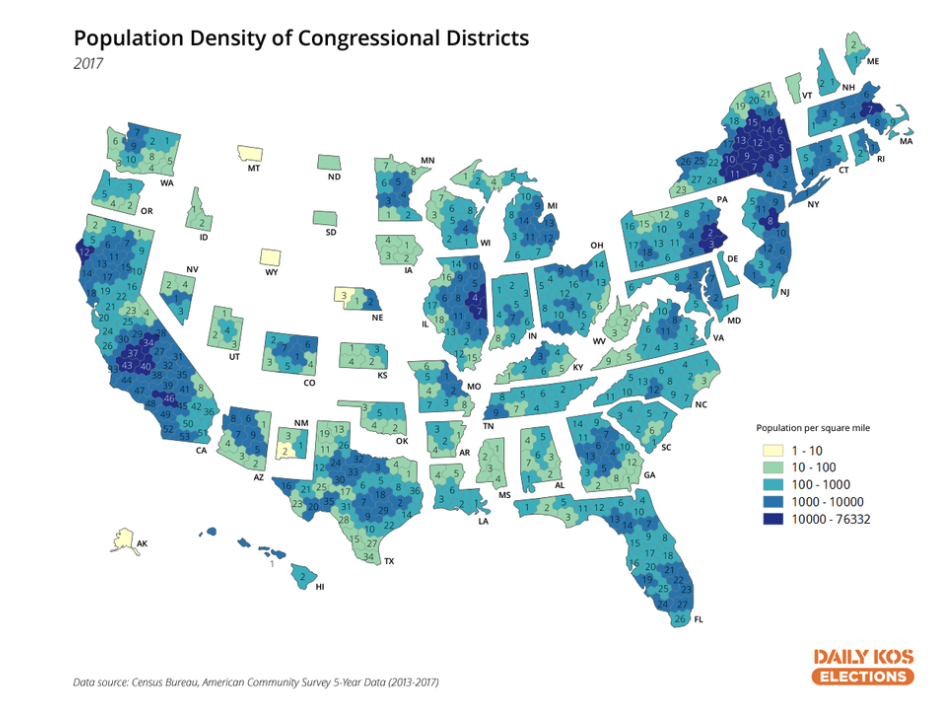
and a 2019 solution to the problem by making each US congressional district the same size and trying to keep the states in the correct shape and relative position to each other, though the locations of the districts themselves within each state are only correct relative to each other. In this case geography is distorted to make areas of roughly equal population more clear.

When looking at much larger regions of the planet the issues are a bit more complex. A 'flat' map can be a good way to see data from all over the planet simultaneously, but it does add in distortions as the earth is sphere-ish, and trying to represent a sphere, or even a portion of it, on a rectangular plane will generate errors. Other tools like Google Earth can be used to map data onto a spherical Earth model, but then there are issues of only being able to see part of the planet at one time.

Coming Next Time

Project 1 Presentations