Lecture 3

Polygon Filling, Point and Line Clipping

(includes text and images from "Computer Graphics: Principles and Practice" by Foley et all)

online, you can click here to see some images created by members of the Electronic Visualization Laboratory here at UIC. Each lecture has a different set of images (collect em all!)

Last time we talked about how line segments are drawn into the frame buffer and began to talk about how polygons are filled in the frame buffer.

Today we will talk more about filling polygons and also discuss clipping ( what happens when the entire line segment or polygon does not lie within the frame buffer.)

From last time the specific polygon filling algorithm:

moving from bottom to top up the polygon
1. find intersections of the scan line with all edges of polygon
2. sort intersections by increasing x coordinate
3. moving through list of increasing x intersections
   parity bit = even (0)
   each intersection inverts the parity bit
   draw pixels when parity is odd (1)
   

makes use of the fact that, similar to the midpoint algorithm, once we have an intersection we incrementally compute the next intersection from the current one. Xi+1 = Xi + 1/m

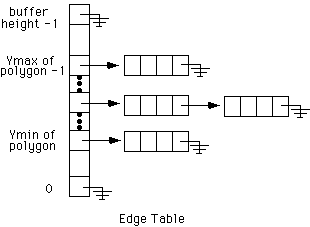
Create a global Edge Table (ET)

• contains all edges sorted by Ymin
• array of buckets - one bucket for each scan line in the polygon
• each bucket has a list of entries stored in increasing X coordinate order (where X is the X value at the Ymin of the line)
• each entry contains Ymax, Xmin (again X at Ymin), 1/m

1. y = minimum Y value in ET (index of first nonempty bucket)
2. set Active Edge Table (AET) to be empty
3. repeat until AET and ET are empty
   1. move edges in ET with Ymin = y into AET (new edges)
   2. sort AET on x (AET will eventually include new and old values)
   3. use list of x coordinates to fill spans
   4. remove entries in AET with ymax = y (edges you are finished with)
   5. add 1 to y (to go to the next scan line)
   6. update X values of remaining entries in AET (add 1/m to account for new y value)

Lots of nagging little details for step 3:

- if intersection is at a noninteger value (say 4.6) is pixel 4 interior? is pixel 5 interior?

if we are outside the polygon (parity is even) then we round up (pixel 5 is interior)
if we are inside the polygon (parity is odd) then we round down (pixel 4 is interior)

- if intersection is at an integer value (say 4.0)

if we are at a left edge then that pixel is interior
if we are at a right edge then that pixel is not interior

- what if more than one vertex shares the same location? (this also handles the situation where you may end up with an odd number of edges in the AET)

bottom vertex of a line segment counts in parity calculation
top vertex of a line segment does not count in parity calculation

- what if 2 vertices define a horizontal edge?

imperfect, but easy, solution is to ignore this edge.

Example:

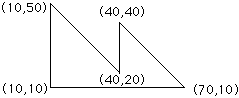
So the ET starts out being ...

------     ----------------     ----------------
| 20 | --> | 50 | 40 | -1 | --> | 40 | 40 | 0  |
------     ----------------     ----------------
------     ----------------     ----------------
| 10 | --> | 50 | 10 | 0  | --> | 40 | 70 | -1 |
------     ----------------     ----------------

and the horizontal line from (10,10) to (70,10) is ignored.

Why would this algorithm be much simpler if the polygon were guarenteed to be convext with no intersecting edges?

Clipping

Since we have a separation between the models and the image created from those models, there can be parts of the model that do not appear in the current view when they are rendered.
pixels outside the clip rectange are clipped, and are not displayed.

can clip analytically - knowing where the clip rectangle is clipping can be done before scan-line converting a graphics primitive (point, line, polygon) by altering the graphics primitive so the new version lies entirely within the clip rectangle

can clip by brute force (scissoring) - scan convert the entire primitive but only display those pixels within the clip rectangle by checking each pixel to see if it is visible.

• clipping a point against a rectangle -> nothing or single point
• clipping a line against a rectangle -> nothing or single line segment
• clipping a rectangle against a rectangle -> nothing or single rectangle
• clipping a convex polygon against a rectangle -> nothing or single single convex polygon
• clipping a concave polygon against a rectangle -> nothing or 1 or more concave polygons

as with scan conversion, this must be done as quickly as possible as it is a very common operation.

Point Clipping

point (X,Y)
clipping rectangle with corners (Xmin,Ymin) (Xmax,Ymax)

point is within the clip rectangle if:

Xmin <= X<= Xmax
Ymin <= Y<= Ymax

Cohen-Sutherland Line Clipping

given a line segment, repeatedly:

1. check for trivial acceptance
   both endpoints within clip rectangle
2. check for trivial rejection
   both endpoints outside clip rectangle IS NOT ENOUGH
   both endpoints off the same side of clip rectangle IS ENOUGH
3. divide segment in two where one part can be trivially rejected

Clip rectangle extended into a plane divided into 9 regions
each region is defined by a unique 4-bit string

• left bit = 1: above top edge (Y > Ymax)
• 2nd bit = 1: below bottom edge (Y < Ymin)
• 3rd bit = 1: right of right edge (X > Xmax)
• right bit = 1: left of left edge (X < Xmin)

• left bit = sign bit of (Ymax - Y)
• 2nd bit = sign bit of (Y - Ymin)
• 3rd bit = sign bit of (Xmax - X)
• right bit = sign bit of (X - Xmin)

(the sign bit being the most significant bit in the binary representation of the value. This bit is '1' if the number is negative, and '0' if the number is positive.)

The frame buffer itself, in the center, has code 0000.

1001 | 1000 | 1010
-----+------+-----
0001 | 0000 | 0010
-----+------+-----
0101 | 0100 | 0110

For each line segment:

1. each end point is given the 4-bit code of its region
2. repeat until acceptance or rejection
   1. if both codes are 0000 -> trivial acceptance
   2. if logical AND of codes is not 0000 -> trivial rejection
   3. divide line into 2 segments using edge of clip rectangle
      1. find an endpoint with code not equal to 0000
      2. move left to right across the code to find a 1 bit -> the crossed edge
      3. break the line segment into 2 line segments at the crossed edge
      4. forget about the new line segment lying completely outside the clip rectangle

The full algorithm is given (in C) in the red book as program 3.7 on p.105.
The full algorithm is given (in Pascal) in the white book as figure 3.41 on p.116.

Coming Next Time

Polygon Clipping and Fun with Circles