Lecture 4

Polygon Clipping and Fun with Circles

(includes text and images from "Computer Graphics: Principles and Practice" by Foley et all)

online, you can click here to see some images created by members of the Electronic Visualization Laboratory here at UIC. Each lecture has a different set of images (collect em all!)

Last time we talked about polygon filling and clipping points and lines.

Today we will talk about clipping polygons and how we deal with circles.

Sutherland-Hodgman Polygon Clipping

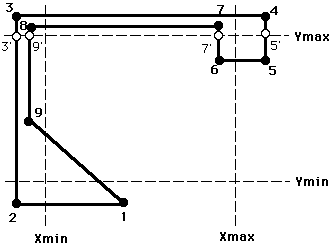
Unlike line-clipping where we selectively clipped against each edge, here we sucessively clip a polygon against all four edges of the clip rectangle

given a polygon with vertices V1, V2, ... Vn
and edges between vertices Vi and Vi+1, and from Vn to V1

for each of the four clipping edges

repeatedly for each vertex V = Vn, V1, V2, ... Vn

given an edge from vertex s to vertex p
assume s has already been dealt with

• if s and p are both inside the clip rectangle -> output p
• if s is inside and p is outside the clip rectangle -> output i (the intersection of edge sp with the clip edge)
• if s and p are both outside the clip rectangle -> output nothing
• if s is outside and p is inside the clip rectangle -> output i (the intersection of edge sp with the clip edge) and then p

output edges become new set of polygon edges

This algorithm can break a single polygon into multiple polygons connected by edges on the boundary of the clipping rectangle for display.

The full algorithm is given (in C) in the red book as program 3.9 on p.114.
The full algorithm is given (in Pascal) in the white book as program 3.49 on p.128.

Example of Polygon Clipping

Clipping on Ymax edge:

• 9-1 : both inside -> add 1
• 1-2 : both inside -> add 2
• 2-3 : keep 2-3' and clip 3'-3 -> add 3'
• 3-4 : both outside -> add nothing
• 4-5 : keep 5'-5 and clip 4-5' -> add 5' and 5
• 5-6 : both inside -> add 6
• 6-7 : keep 6-7' and clip 7'-7 -> add 7'
• 7-8 : both outside -> add nothing
• 8-9 : keep 9'-9 and clip 8-9' -> add 9' and 9
• 9-1 : both inside -> add 1
• returning 1,2,3',5',5,6,7',9',9 as the new vertex sequence

the new vertex sequence is then checked against the Ymin edge and so on through the Xmax edge and the Xmin edge

2 More Examples

Drawing Circles

The algorithm used to draw circles is very similar to the Midpoint Line algorithm.

8 way-symmetry - for a circle centered at (0,0) and given that point (x,y) is on the circle, the following points are also on the circle:

(-x, y)
( x,-y)
(-x,-y)
( y, x)
(-y, x)
( y,-x)
(-y,-x)

So it is only necessary to compute the pixels for 1/8 of the circle and then simply illuminate the appropriate pixels in the other 7/8.

Given a circle centered at (0,0) with radius R:

        R² = X² + Y²
        F(X,Y) = X² + Y² - R²

We choose to work in the 1/8 of the circle (45 degrees) from x=0 (y-axis) to x = y = R/sqrt(2) (45 degrees clockwise from the y-axis.)

so for any point (X_i,Y_i) we can plug X_i,Y_i into the above equation and

        F(X_i,Y_i) = 0 -> (X_i,Y_i) is on the circle
        F(X_i,Y_i) > 0 -> (X_i,Y_i) is outside the circle
        F(X_i,Y_i) < 0 -> (X_i,Y_i) is inside the circle

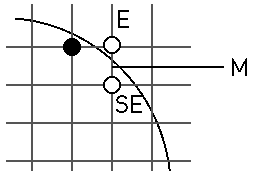
Given that we have illuminated the pixel at (Xp,Yp) we will next either illuminate

the pixel to the EAST (Xp + 1,Yp)
or the pixel to the SOUTHEAST (Xp+ 1,Yp - 1)

We again create a decision variable d set equal to the function evaluated at the midpoint (Xp+ 1,Yp - 0.5)

d = F(Xp + 1,Yp - 0.5)
We plug the midpoint into the above F() for the circle and see where the midpoint falls in relation to the circle.

d > 0 (midpoint is outside) -> pick SOUTHEAST pixel
d < 0 (midpoint is inside) -> pick EAST pixel
d = 0 (midpoint is on circle) -> ***CHOOSE*** to pick SOUTHEAST pixel

dcurrent = F(Xp + 1, Yp - 0.5)
dcurrent = (Xp + 1)² + (Yp - 0.5)² - R²
dcurrent = Xp² + 2Xp + 1 + Yp² - Yp + 0.25 - R²

if the EAST pixel is chosen then:

        dnew = F(Xp + 2, Yp - 0.5)
        dnew = (Xp + 2)² + (Yp - 0.5)² - R²
        dnew = Xp² + 4Xp + 4 + Yp² - Yp + 0.25 - R²

        dnew - dcurrent = deltaE = 2Xp + 3

if the SOUNTEAST pixel is chosen then:

        dnew = F(Xp + 2, Yp - 1.5)
        dnew = (Xp + 2)² + (Yp - 1.5)² - R²
        dnew = Xp² + 4Xp + 4 + Yp² - 3Yp + 2.25 - R²

        dnew - dcurrent = deltaSE = 2Xp - 2Yp + 5

Unlike the algorithm for lines, deltaE and deltaSE are not constant.

initial point (Xo,Yo) is known to be (0,R)
so initial M is at (1, R - 0.5)
so initial d = F(1, R - 0.5)

        = 1² + (R - 0.5)² - R²
        = 1 + R² - R + 0.25 - R²
        = 1.25 - R

unfortunately while deltaSE and deltaE are integral, d is still a real variable, not an integer so:

h = d - 0.25
h is initialized as 1 - R (instead of 1.25 - R)
h is compared to as h < 0.25 (instead of d< 0)

but since h starts off as an integer (assuming an integral R) and h is only incremented by integral amounts (deltaE and deltaSE) we can ignore the 0.25 and compare h < 0.

X = 0;
Y = radius;
d = 1 - radius;
draw8Points(X, Y);
while(Y > X)

if (d< 0)

add 2 * X + 3 to d
add 1 to X

else

add 2 * (X-Y) + 5 to d
add 1 to X
subtract 1 from Y

draw8Points(X, Y);

The full algorithm is given (in C) in the red book as program 3.4 on p.83.
The full algorithm is given (in Pascal) in the white book as figure 3.16 on p.86.

This is still somewhat bad in that there is a multiplication to compute the new value of the decision variable. The book shows a more complicated algorithm which does this multiplication only once.

ellipses F(x,y) = b^2 X^2 + a^2 Y^2 - a^2 b^2 = 0 are handled in a similar manner, except that 1/4 of the ellipse must be dealt with at a time and that 1/4 must be broken into 2 parts based on where the slope of the tangent to the ellipse is -1 (in first quadrant.)

Filling Circles

Circles have the advantage of being convex polygons, so each scan line will have a single span.

The span extrema can be computed using the same method as was used to draw the pixels on the boundary of the circle, computing them for 1/8 of the circle and using 8-way symetry to get the other 7/8. These extrema can then be stored in an array of Xmin and Ymin indexed by Y

Coming Next Time

At this point we have discussed the primitive operations to set the contents of the frame buffer. Now we are going to go up a level of abstraction and look at how geometric transformations are used to alter the view of a 2D model: how we can translate, scale, and rotate the model, and how transformations affect what the viewport 'sees.' Geometric Transformations

I --->highly<--- recommend looking over section 5.1 in the textbook which reviews matrices and vectors, before coming to class next Tuesday. Along with the review in the discussion section, this should prepare you for the coming of matrices.