Lecture 5

Programming assignment #2 is now available

Geometric Transformations

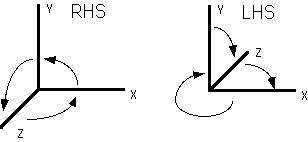
(includes text and images from "Computer Graphics: Principles and Practice" by Foley et all)

online, you can click here to see some images created by members of the Electronic Visualization Laboratory here at UIC. Each lecture has a different set of images (collect em all!)

Today we will talk about how transforms using matrices are used to affect the position, size, and orientation of polygons in the scene.

Section 5.1 in the text gives a review of vectors and matrices.

Transforms are applied to vertices and then the edges are drawn between the new vertices and the new polygon can then be filled.

Coordinate Systems

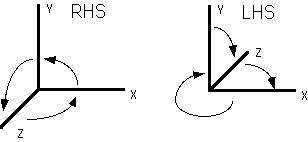
Right Hand Coordinate System (RHS)
Z is coming out of the page

Counterclockwise rotations are positive
if we rotate about the X axis : the rotation Y->Z is positive
if we rotate about the Y axis : the rotation Z->X is positive
if we rotate about the Z axis : the rotation X->Y is positive

Left Hand Coordinate System (LHS)
Z is going into the page

Clockwise rotations are positive
if we rotate about the X axis : the rotation Y->Z is positive
if we rotate about the Y axis : the rotation Z->X is positive
if we rotate about the Z axis : the rotation X->Y is positive

so basically its the same thing ...

Translation

point (X,Y) is to be translated by amount Dx and Dy to location (X',Y')
X' = Dx + X
Y' = Dy + Y

or P' = T + P where

      _   _
P' = |  X' |
     |  Y' |
      -   -
      _    _
T  = |  Dx  |
     |  Dy  |
      -    -
      _   _
P  = |  X  |
     |  Y  |
      -   -

Scaling

point (X,Y) is to be scaled by amount Sx and Sy to location (X',Y')
X' = Sx * X
Y' = Sy * Y

or P' = S * P where

      _   _
P' = |  X' |
     |  Y' |
      -   -
      _       _
S  = |  Sx  0  |
     |  0   Sy |
      -       -
      _   _
P  = |  X  |
     |  Y  |
      -   -

scaling is performed about the origin (0,0) not about the center of the line/polygon/whatever

Scale > 1 enlarge the object and move it away from the origin.
Scale = 1 leave the object alone
Scale< 1 shrink the object and move it towards the origin.

uniform scaling: Sx = Sy
differential scaling Sx != Sy -> alters proportions

Rotation

point (X,Y) is to be rotated about the origin by angle theta to location (X',Y')
note that this does involve sin and cos which are much more costly than addition or multiplication
X' = X * cos(theta) - Y * sin(theta)
Y' = X * sin(theta) + Y *cos(theta)

or P' = R * P where

      _   _
P' = |  X' |
     |  Y' |
      -   -
      _                       _
R  = |  cos(theta) -sin(theta) |
     |  sin(theta) cos(theta)  |
      -                       -
      _   _
P  = |  X  |
     |  Y  |
      -   -

rotation is performed about the origin (0,0) not about the center of the line/polygon/whatever

Where does this matrix come from?
(X,Y) is located r away from (0,0) at a CCW angle of phi from the X axis.
(X',Y') is located r away from (0,0) at a CCW angle of theta+phi from the X axis.

Since rotation is about the origin, (X',Y') must be the same distance from the origin as (X,Y).

from trig ...
X = r * cos(phi)
Y = r * sin(phi)

X' = r * cos(theta+phi)
Y' = r * sin(theta+phi)

since
cos(a+b) = cos(a) * cos(b) - sin(a) * sin(b)
sin(a+b) = sin(a) * cos(b) + cos(a) * sin(b)

X' = r * cos(theta) * cos(phi) - r * sin(theta) * sin(phi)
Y' = r * sin(theta) * cos(phi) + r * cos(theta) * sin(phi)

X' = X * cos(theta) - Y * sin(theta)
Y' = X * sin(theta) + Y * cos(theta)

Homogeneous Coordinates

Want to be able to treat all 3 transformations (translation, scaling, rotation) in the same way - as multiplications

each point given a third coordinate (X, Y, W)

two triples (X,Y,W) and (X',Y',W') represent the same point if they are multiples of each other e.g. (1,2,3) and (2,4,6)

at least one of the three coordinates must be nonzero

if W is 0 then the point is at infinity if W is nonzero we can divide the triple by W to get the cartesian coordinates of X and Y which will be identical for triples representing the same point (X/W, Y/W, 1)

new translation: point (X,Y) is to be translated by amount Dx and Dy to location (X',Y')
X' = Dx + X
Y' = Dy + Y

or P' = T * P where

      _   _
P' = |  X' |
     |  Y' |
     |  1  |
      -   -
      _        _
T  = |  1 0 Dx  | = T(Dx,Dy)
     |  0 1 Dy  |
     |  0 0  1  |
      -        -
      _   _
P  = |  X  |
     |  Y  |
     |  1  |
      -   -

new scaling:

      _   _
P' = |  X' |
     |  Y' |
     |  1  |
      -   -
      _        _
S  = |  Sx 0 0  | = S(Sx,Sy)
     |  0 Sy 0  |
     |  0  0 1  |
      -        -
      _   _
P  = |  X  |
     |  Y  |
     |  1  |
      -   -

new rotation:

      _   _
P' = |  X' |
     |  Y' |
     |  1  |
      -   -
      _                         _
R  = |  cos(theta) -sin(theta) 0 | = R(theta)
     |  sin(theta)  cos(theta) 0 |
     |       0           0     1 |
      -                         -
      _   _
P  = |  X  |
     |  Y  |
     |  1  |
      -   -

Composition of 2D Transformations

Instead of applying several transformations matrices to a point we want to use the transformations to produce 1 matrix which can be applied to the point.

In the simplest case we want to apply the same type of transformation (translation, rotation, scaling) more than once.

translation is additive as expected
scaling is multiplicative as expected
rotation is additive as expected

But what if we want to combine different types of transformations?

a very common reason for doing this is to rotate a polygon about an arbitrary point (e.g. the center of the polygon) rather than around the origin.

Translate so that P1 is at the origin T(-Dx,-Dy)
Rotate R(theta)
Translate so that the point at the origin is at P1 T(Dx,Dy)

note the order of operations here is right to left P' = T(Dx,Dy) * R(theta) * T(-Dx,-Dy) * P

The matrix that results from these 3 steps can then be applied to all of the points in the polygon.

another common reason for doing this is to scale a polygon about an arbitrary point (e.g. the center of the polygon) rather than around the origin.

Translate so that P1 is at the origin
Scale
Translate so that the point at the origin is at P1

How do we determine the 'center' of the polygon?

• specifically define the center (e.h. the center of mass)
• average the location of all the vertices
• take the center of the bounding box of the polygon

Window to Viewport

Generally user's prefer to work in world-coordinates.

1 unit can be 1 micron
1 unit can be 1 meter
1 unit can be 1 kilometer
1 unit can be 1 mile

These coordinates must then be translated to screen coordinates to be displayed in a rectangular region of the screen called the viewport

The objects are in world coordinates (with n dimensions)
The viewport is in screen coordinates (with n=2)

Want one matrix that can be applied to all points:
rectangular area of world from (Xmin,Ymin) to (Xmax,Ymax) - world-coordinate window
rectangular area of screen from (Umin,Vmin) to (Umax,Vmax) - viewport

need to rescale the world-coordinate rectangle to the screen rectangle

1. translate world-coordinate window to the origin of the world coordinate system.
2. rescale the window to the size and aspect ratio of the viewport.
3. translate the viewport to its position on the screen in the screen coordinate system.

Pscreen = M * Pworld
M = T(Umin,Vmin) * S(deltaU/deltaX, deltaV/deltaY) * T(-Xmin, -Ymin)

3D Transformations

Similar to 2D transformations, which used 3x3 matrices, 3D transformations use 4X4 matrices (X, Y, Z, W)

3D Translation: point (X,Y,Z) is to be translated by amount Dx, Dy and Dz to location (X',Y',Z')
X' = Dx + X
Y' = Dy + Y
Z' = Dz + Z

or P' = T * P where

      _   _
P' = |  X' |
     |  Y' |
     |  Z' |
     |  1  |
      -   -
      _          _
T  = |  1 0 0 Dx  | = T(Dx,Dy,Dz)
     |  0 1 0 Dy  |
     |  0 0 1 Dz  |
     |  0 0 0  1  |
      -          -
      _   _
P  = |  X  |
     |  Y  |
     |  Z  |
     |  1  |
      -   -

3D scaling:

      _   _
P' = |  X' |
     |  Y' |
     |  Z' |
     |  1  |
      -   -
      _            _
S  = |  Sx 0  0  0  | = S(Sx,Sy,Sz)
     |  0  Sy 0  0  |
     |  0  0  Sz 0  |
     |  0  0  0  1  |
      -            -
      _   _
P  = |  X  |
     |  Y  |
     |  Z  |
     |  1  |
      -   -

3D rotation:
for 3D rotation we need to pick an axis to rotate about. The most common choices are the X-axis, the y-axis, and the z-axis

      _   _
P' = |  X' |
     |  Y' |
     |  Z' |
     |  1  |
      -   -
      _                           _
Rz = |  cos(theta) -sin(theta) 0 0 | = Rz(theta)
     |  sin(theta)  cos(theta) 0 0 |
     |       0           0     1 0 |
     |       0           0     0 1 |
      -                           -
      _                           _
Rx = |  1     0           0      0 | = Rx(theta)
     |  0 cos(theta) -sin(theta) 0 |
     |  0 sin(theta)  cos(theta) 0 |
     |  0     0           0      1 |
      -                           -
      _                           _
Ry = | cos(theta)  0 sin(theta)  0 | = Ry(theta)
     |     0       1      0      0 |
     | -sin(theta) 0 cos(theta)  0 |
     |     0       0      0      1 |
      -                           -
      _   _
P  = |  X  |
     |  Y  |
     |  Z  |
     |  1  |
      -   -

In OpenGL translation, rotation, and scaling are performed using commands such as:
glTranslate{fd}(X,Y,Z) - glTranslatef(1.0, 2.5, 3.0)
glRotate{df}(Angle, X, Y, Z) - glRotatef(60.0, 0.0, 0.0, 1.0)
glScale{df}(X, Y, Z) - glScalef(1.0, 1.5, 2.0)

Composition is handled in a similar way to the 2D case

Coming Next Time

More Geometric Transformations