online, you can click here to see some images created by members of the Electronic Visualization Laboratory here at UIC. Each lecture has a different set of images (collect em all!)
Last time we talked about 2D and 3D transformations and how those transformations affect objects in the scene.
Today we will talk more about this, and discuss how polygons are usually formed into hierarchies of more meaningful objects. We will also briefly discuss how fonts are handled.
Last time we talked about transforms in terms of an object (polygon, line, point) in the same coordinate system of the world, that is (0,0) for the object is the same as (0,0) for the world.
An alternative (and usually preferable) way is for each object to have its own local coordinate system separate from all of the other objects and the world coordinate system. This allows each object to be created separately and then added into the world, using transformations to place the object at the appropriate point.
This is especially useful when you build larger objects out of reusable smaller objects.
For example we could have a square with 2 unit long sides and the center of the square at its origin.
The vertices of the square are: (-1,-1) ( 1,-1) ( 1, 1) (-1, 1)
This is nice because the center of the square is where we probably want the center of rotation/scaling to be. We can rotate/scale it where it is and then translate it where it belongs in the world (e.g. T(5,5) to move the center to (5,5) in world-space)
When we design the object we place the center of rotation/scaling where we wish it to be. For a wheel the center of rotation would be where the axel is to be attached, for a hinged gate the center would be at the hinge.
Each object must then be translated/rotated/scaled (from its local co-ordinate system) to place it at the proper location in the world (in the world co-ordinate system).
Say we are drawing an automobile and we want to draw the 4 tires. We can either draw each of the 4 tires independently at the appropriate location, or draw the same tire centered at its origin 4 times, and each time move it to the appropriate location in the world.
Some OpenGL code to create a solar system with a single sun and a single planet in orbit about it. We will bend the laws of physics slightly and say that the planet is orbiting about the center of the sun rather than having the objects in orbit about their shared center of mass. We also assume a circular orbit and that the plane of the solar system matches the Y=0 plane
We
place the sun at 0,0,0 at it will be a sphere of radius 1
The planet has a radius of 0.2 and orbits the sun at a radius of 2
The planet rotates about its axis once per day
The planet revolves around the sun once each year
glLoadIdentity(); //reset the matrix to the identity matrix
glPushMatrix();
glRotatef(yearPercentage, 0.0, 1.0, 0.0);
glTranslatef(2.0, 0.0, 0.0);
glRotatef(dayPercentage, 0.0, 1.0, 0.0);
drawSphere(0.2) // user defined function to draw the planet
glPopMatrix();
If you think about the single coordinate system then the operations on the matrix are done in the REVERSE order from which they are called:
Note:
dayPercentage is the amount the planet rotates about ITS center.
yearPercentage is the amount the planet rotates about the center of the
sun.
if the matrix operations are not performed in reverse order then the year and day rotation percentages get reversed.
If you think about each object having its own coordinate system then the operations on the matrix are done in the SAME order as they are called:
Either way of thinking about it is equivalent, and irregardless of how you think about it, that is how OpenGL function calls must be issued.
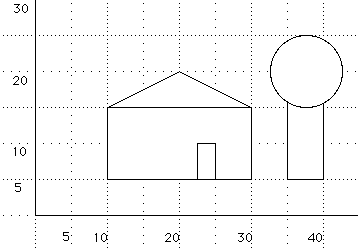
Say you have three polygonal drawing functions available to you:
How
can I draw the following scene?

Single polygons are generally too small to be of interest ... its hard to think of a single polygon as an 'object' unless you are writing Tetris(tm).
Even in a 2D world it is more convenient to think of objects which are a collection of polygons forming a recognizable shape: a car, a house, or a laser-toting mutant monster from Nebula-9. This object can then be moved/rotated/scaled as a single entity, at least at the conceptual level.
This is especially true in a 3D world where you need more than one (planar) polygon to create a 3D object.
Creating an object polygon by polygon is very slow when you want to create a very large complex object. On the other hand it does give you much more control over the object than creating it from higher-level primitives (cube, cone, sphere)
The
following two examples are from Silicon Graphics' OpenInventor(tm) a
library which sits on top of OpenGL and allows higher-level objects to
be created. The first shows a tree constructed from a cube and a cone.
The second shows the same tree but constructed from triangular polygons.
note, triangular polygons are often used instead of 4-sided ones because the 3 vertices in the triangle are guaranteed to form a plane, while the 4 vertices of a 4-sided polygon may not all fall in the same plane which may cause problems later on.
Hierarchies are typically stored as Directed Acyclic Graphs, that is they are trees where a node can have multiple parents as long as no cycle is generated.
Hierarchies store all information necessary to draw an object:
Hierarchies are useful when you want to be able to manipulate an object on multiple levels:
With a car the wheels should rotate but if the car body is moving then the wheels should also be moving the same amount.
An object hierarchy gives a high degree of encapsulation.
An object heierarchy allows inheritance
For example, at the top of the hierarchy the object could be set to draw only as a wireframe, or with different lighting models, or different colours, or different texture maps. This would then be inherited by the sub-objects and not have to be explicitely set each of them.
Hierarchies increase modularity.
Hierarchies decrease storage space
Hierarchies make it easy to propagate changes.
Hierarchies are common in 'real life' so it can be easier to model hierarchical things in a hierarchy.
How can I redraw the house and tree scene to make better use of objects?
Text is handled in one of two ways.
bitmaps:
rectangular array of 0s and 1s
00000000
00011000
00100100
01000010
01111110
01000010
01000010
01000010
polygons:
OpenGL provides minimal font support - only bitmapped fonts. Fortunately there are free 3D fonts available such as the Hershey library.
3D Graphics and More Matrices than you can Possibly Imagine