Results of the midterm are available through the Current Gradesheet.
Last week we had the midterm, but before that we talked about how to take 2D and 3D scenes and draw them on a 2D surface.
For the rest of this course we will be discussing how to make these images more interesting. This will involve talking about light, illumination, colour, and shading, and how we deal with objects that occlude other objects.
Today we are going to talk about light and colour, and have a slightly overdue discussion about the nature of human vision ... in future weeks we will deal with the more sophisticated concepts of illumination and shading.
online, you can click here to see some images created by members of the Electronic Visualization Laboratory here at UIC. Each lecture has a different set of images (collect em all!)


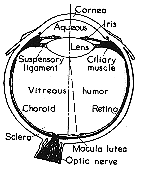
Light is focused by the cornea and the lens onto the retina at the back of the eye.
Vitreous humor - liquid inside the cornea is close to water, and has the same index of refraction as water. If we are under water the light is not refracted, but it is refracted if we are not in water.
Light passing through the center of the cornea and lens hits the fovea (or Macula).
Human eye has 2 types of photosensitive receptors: cones and rods
cones
rods
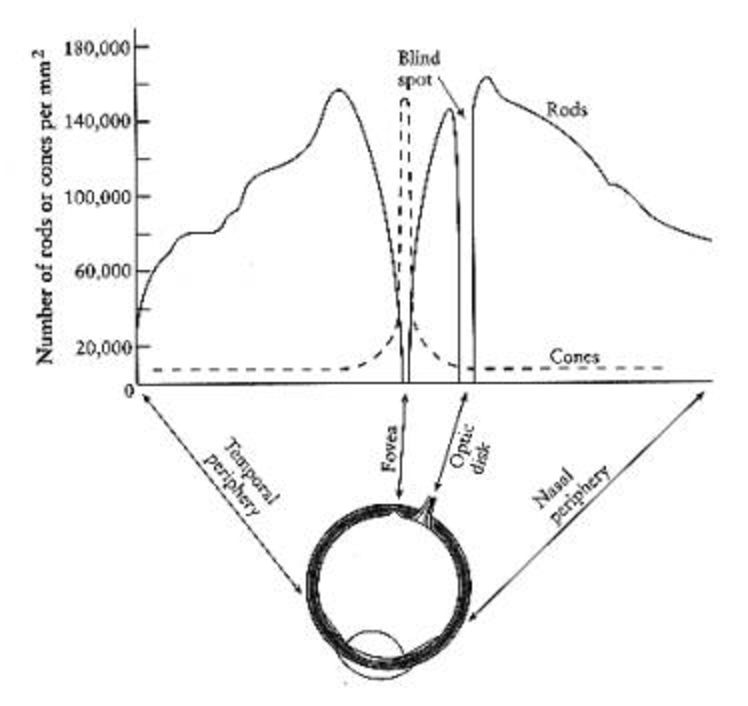
The cones are highly concentrated at the fovea and quickly taper off around the retina. For colour vision we have the greatest acuity at the fovea, or approximately at the center of out field of vision. Visual acuity drops off as we move away from the center of the field of view. However, we are very sensitive to motion on the periphery of our vision, so we can see movement even if we can't see what is moving.
The rods are highly concentrated 10-20 degrees on both sides of the fovea, but almost none are at the fovea itself - which is why if you are stargazing and want to see something dim you can not look directly at it.
There is also the optic nerve which is 10-20 degrees away from the fovea which connects your eye to your brain. This is the blind spot where there are no cones and no rods. We can not see anything at this point though we are so used to this that we do not notice it unless we try to see the blind spot.
Bill Sherman's diagram
Try the following link if you want to see (or not see) your blind spot: http://serendip.brynmawr.edu/bb/blindspot1.html
What happens when we walk from a bright area into a dark area, say into a movie theatre? When we are outside the rods are saturated from the brightness. The cones which operate better at high illumination levels provide all the stimulous. When we walk into the darkened theatre the cones don't have enough illumination to do much good, and the rods take time to desaturate before they can be useful in the new lower illumination environment.
It takes about 20 minutes for the rods to become very sensitive, so dark adjust for about 20 minutes before going stargazing.
Since the cones do not operate well at low light intensities we can not see colour in dim light as only the rods are capable of giving us information. The rods are also more sensitive to the blue end of the spectrum so it is especially hard to see red in the dark (it appears black).
Here is one of my favourite optical illusions:
http://www.ritsumei.ac.jp/~akitaoka/saishin-e.html
There
are several pages of optical illusions on the web:
http://www.ads-online.on.ca/illusion/directory.html
and of course there's always M.C. Escher ...
http://www.worldofescher.com/gallery/
Computer graphics is based on illusion, from the R, G, and B phosphors on a CRT to creating an illusion of 3D on a (relatively) flat CRT screen.
no colour, only greyscale with 0 as black, and 1 as white.
quantity of light or intensity of light is the only parameter
To human beings, brightness (perceived intensity) has a logarithmic scale, not a linear scale.
CRTs can not get completely black due to light reflection within the tube. Minimum values range from 0.005 to 0.025 of the maximum intensity.
ration of maximum to minimum intensity is the dynamic range of the CRT.
for n+1 intensities and a minimum intensity of Io and a maximum intensity of 1, the ratio of succeeding intensities is:
(1/n) (n-j)/n
r = (1/Io) and Ij = Io
For
10 intensities from 0.1 to 1
r = 1.292 and the 10 intensities are:
0.1 0.13 0.17 0.21 0.28 0.36 0.46 0.59 0.77 1.0
whereas
a linear scale would be:
0.1 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90 1.0
The number of distinct intensities needed for smooth continuous tone depends on the dynamic range of the device. The human eye can not distinguish between intensities with a ratio of less than 1.01.
so with 1/Io as the dynamic range, w set r = 1.01 and want to find n.
(1/n)
1.01 = (1/Io)
Through
the magick of logarithms (which I am not even going to attempt to
remember) we can find the following: for a CRT with dynamic range of 50
to 200, 400-530 intensities are needed
for a photographic print with range 100, 465 intensities are needed
for a photographic slide with range 1000, 700 intensities are needed
hue:
saturation:
lightness:
brightness:
a good way to learn about these terms is to load up Adobe Photoshop(tm) and play with the controls.
Why
do CRTs have red, green, and blue phosphors?
Currently believed there are three kinds of cones in the human eye, one
attuned to red, one to green, and one to blue (Young and Helmholtz) ...
but this is still being debated.
Light is electromagnetic energy with wavelengths from 400nm - 700nm
peak
red response at 580nm (reddish-yellow)
peak green response at 545nm (greenish-yellow)
peak blue response at 440nm
So the idea is to add an amount of red and an amount of green and an amount of blue to produce a wide range of colours.
Unfortunately we can not generate all the colours that the eye can see using an RGB CRT. We also can not generate all the colours that the eye can see using photgraphics film (though it can display a larger part of the visible spectrum than a monitor)
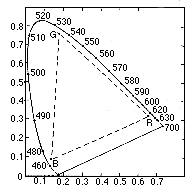
This is the CIE Chromaticity diagram developed in 1931. If luminance is included this becomes a 3D cone, by normalizing we reduce the cone to a plane (the X + Y + Z = 1 plane). Chromaticity depends on dominant wavelength (hue) and saturation only. As with homogeneous coordinates, different luminances are mapped onto the same point on the plane. So this plane DOES NOT contain all the possible colours as colour also depends on luminance (lightness or brightness).
Unfortunately you cant mix positive amounts of the three primary colours (red, green, and blue) to create all of the possible colours that we can see. So for the diagram above there are three primary colours X, Y, and Z are defined so that you can add X and Y and Z together to get all of the possible colours - so by definition X, Y, and Z are not be red, green, and blue and the colour matching functions (the curves) of X, Y, and Z are not the curves of red, green, and blue.
(for athorough explanation of the x,y axis, you should see section 13.2.2 (p579) in the Foley et al text)
The curvy region is the colours we can see. The boundary stretches from purple at 400 near the origin to green at 510 near the top of the y axis to red at 700 at the far right.
White light is defined to exist near the center of the space.
Given 2 points within the region the colours on the line between those 2 points are mixtures of those two colours.
If you have a point (colour) in the space and draw a line from the nearest boundary through the point to the white-light center you can determine the dominant wavelength (hue) and saturation. The dominant wavelength is the point where the boundary is crossed, and the saturation is a measure of how close the point is to the white-light center from the boundary. Some colours (in the purple to red range) do not have a dominant wavelength as the lower ende of the curve does not represent spectral colours. these non-spectral colours are defined as being complementary colours to the dominant wavelength on the other side.
Complementary colours exist on opposite sides of the white-light center, whose mixture yields the white-light center.
The triangle shows the colours we can make by adding R, G, and B. Different hardware has different triangles allowing us to compare the gamuts (colour ranges) of different devices on the same diagram.
One other factor that can be important in computer graphics is the decay rate of certain colours. We have talked about how the graphics get refreshed on the screen at 60 or 96 or 120 times per second, but depending on the chemical or physical processes inside the display hardware, the previous image may not totally be replaced by the new image. This can generate ghosting.
More info on the CIE diagram can be found here: http://hyperphysics.phy-astr.gsu.edu/hbase/vision/cie.html
RGB
RGB has three primary colours Red Green Blue, each of which ranges from 0 to 1, which are added together to form the final colour.
black is at the origin (0,0,0)
if the r,g,b values are identical then the resulting colour is grey, ranging from black (0,0,0) to white (1,1,1).
(1,0,0) -> red
(0,1,0) -> green
(0,0,1) -> blue
(1,1,0) -> yellow
(1,0,1) -> magenta
(0,1,1) -> aqua
Here is an image from Cornell (http://www.graphics.cornell.edu/KOC95/color/color.html) showing how Red, Green, and Blue are used to create a colour image.

CMY
CMY has three primary colours Cyan Magenta Yellow (the complements of red, green and blue) each of which ranges from 0 to 1, which are subtracted from white to form the final colour.
cyan
is white minus red, leaving only green and blue
magenta is white minus green, leaving only red and blue
yellow is white minus blue, leaving only red and green
white is at the origin (1,1,1)
(0,1,1) -> red
(1,0,1) -> green
(1,1,0) -> blue
(0,0,1) -> yellow
(0,1,0) -> magenta
(1,0,0) -> aqua
To convert between RGB and CMY:
_ _ _ _ _ _
| C | | 1 | | R |
| M | = | 1 | - | G |
| Y | | 1 | | B |
- - - - - -
_ _ _ _ _ _
| R | | 1 | | C |
| G | = | 1 | - | M |
| B | | 1 | | Y |
- - - - - -
CMYK adds blacK as a fourth parameter to CMY
YIQ
recoding of RGB for US television broadcasts
Y = luminance, and is the only component shown on black and white TVs.
_ _ _ _ _ _
| Y | | 0.299 0.587 0.114 | | R |
| I | = | 0.596 -0.275 -0.321 | - | G |
| Q | | 0.212 -0.528 0.311 | | B |
- - - - - -
HSV (HSB)
Hue
Saturation
Value (Brightness)
HLS
Hue
Lightness
Saturation
There is a lot of research out there on how to effectively use colour, and many, many examples of how not to use colour.
8
percent of men
0.5 percent of women
Here is another image from Cornell (http://www.graphics.cornell.edu/KOC95/color/color.html) showing how the previous image would look for 3 of the more common types of colour blindness.

Colour is a very powerful tool - and therefor a dangerous tool. Aside from issues of colour blindness and other physiological issues we looked at with the optical illusions, there is a lot of cultual baggage associated with colour. If colour is important in the computer graphics that you are doing (eg scientific visualizations) you need to learn about colour of work with someone who knows about colour.
Here
is a very good starting point: Interaction of Color by Josef
Albers
We determine depth through a combination of 2D and 3D cues, which is how many of the optical illusions at the beginning work, and how we can play 'Doom' and get a sense of 3D space and motion.
Some people do not have stereo vision so all of their depth cues are 2D, and they do very well with only these 2D cues.
There are eight 2D depth cues:
Overlap Closer objects cover parts of objects that are further away.
Apparent Size As an object moves towards us it gets larger in our retina but we do not perceive it getting bigger. We understand that it isn't changing its size as it moves.
Differential Size If we know that two objects are the same size and one appears to be smaller than the other then the smaller one is further away.
Linear Perspective Parallel lines converge to the vanishing point as they go off in the distance.
Motion Parallax Objects that are closer will move 'more' or 'faster' than objects that are further away.
Aerial Perspective Fog/Smog/Dust/Dirt in the air make objects that are further away appear less distinct.
Texture You can only discern textures when an object is near, otherwise the surface appears uniform.
Shading and Lighting for a lot of small reasons.
The
dominant cue at long distances is differential size
The dominant cue at intermediate distances is motion parallax
The dominant cue within 12" is stereo vision
Visible-Surface Determination
last revision 10/31/00