Last time we talked about visible surfaces and discussed the major visible-surface determination algorithms: back-face culling, the depth buffer, and Warnock's algorithm.
Today we are going to discuss some more algorithms for determining visible surfaces.
online, you can click here to see some images created by members of the Electronic Visualization Laboratory here at UIC. Each lecture has a different set of images (collect em all!)
The idea here is to go back to front drawing all the objects into the frame buffer with nearer objects being drawn over top of objects that are further away.
Simple algorithm:
This algorithm would be very simple if the z coordinates of the polygons were guaranteed never to overlap. Unfortunately that is usually not the case, which means that step 2 can be somewhat complex.
Any polygons whose z extents overlap must be tested against each other.
We start with the furthest polygon and call it P. Polygon P must be compared with every polygon Q whose z extent overlaps P's x extent. 5 comparisons are made. If any comparison is true then P can be written before Q. If at least one comparison is true for each of the Qs then P is drawn and the next polygon from the back is chosen as the new P.
If all 5 tests fail we quickly check to see if switching P and Q will work. Tests 1, 2, and 5 do not differentiate between P and Q but 3 and 4 do. So we rewrite 3 and 4
3
- is Q entirely on the opposite side of P's plane from the viewport.
4 - is P entirely on the same side of Q's plane as the viewport.
If either of these two tests succeed then Q and P are swapped and the new P (formerly Q) is tested against all the polygons whose z extent overlaps it's z extent.
If these two tests still do not work then either P or Q is split into 2 polygons using the plane of the other. These 2 smaller polygons are then put into their proper places in the sorted list and the algorithm continues.
beware of the dreaded infinite loop.
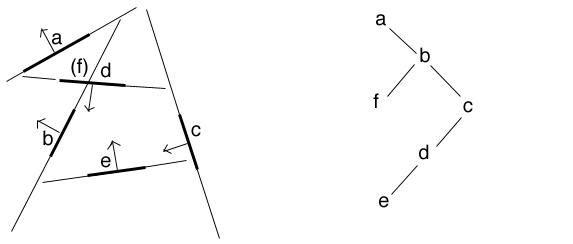
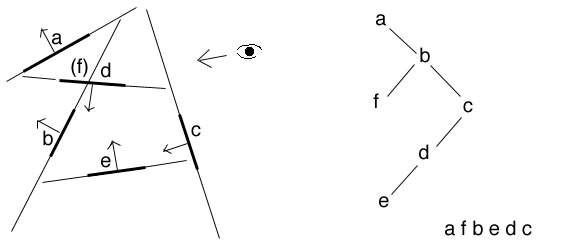
Another popular way of dealing with these problems (especially in games) are Binary Space Partition trees. It is a depth sort algorithm with a large amount of preprocessing to create a data structure to hold the polygons.
First generate a 3D BSP tree for all of the polygons in the scene
Then display the polygons according to their order in the scene
Each node in the tree is a polygon. Extending that polygon generates a plane. That plane cuts space into 2 parts. We use the front-facing normal of the polygon to define the half of the space that is 'in front' of the polygon. Each node has two children: the front children (the polygons in front of this node) and the back children (the polgons behind this noce)
In doing this we may need to split some polygons into two.
Then when we are drawing the polygons we first see if the viewpoint is in front of or behind the root node. Based on this we know which child to deal with first - we first draw the subtree that is further from the viewpoint, then the root node, then the subtree that is in front of the root node, recursively, until we have drawn all the polygons.
Compared to depth sort it takes more time to setup but less time to iterate through since there are no special cases.
If the position or orientation of the polygons change then parts of the tree will need to be recomputed.
here is an example originally by Nicolas Holzschuch showing the construction and use of a BSP tree for 6 polygons.
This is an extension of the algorithm we dealt with earlier to fill polygons one scan line at a time. This time there will be multiple polygons being drawn simultaneously.
Again we create a global edge table for all non-horizontal edges sorted based on the edges smaller y coordinate.
Each entry in the table contains:
and a new entry
In the scan line algorithm we had a simple 0/1 variable to deal with being in or out of the polygon. Since there are multiple polygons here we have a Polygon Table.
The Polygon Table contains:
Again the edges are moved from the global edge table to the active edge table when the scan line corresponding to the bottom of the edge is reached.
Moving across a scan line the flag for a polygon is flipped when an edge of that polygon is crossed.
If
no flags are true then nothing is drawn
If one flag is true then the colour of that polygon is used
If more than one flag is true then the frontmost polygon must be
determined.
Below
is an example from the textbook (figure red:13.11, white:15.34)
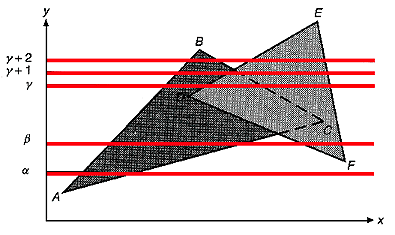
Here there are two polygons ABC and DEF
Scan Line AET contents Comments
--------- ------------ --------
alpha AB AC one polygon
beta AB AC FD FE two separate polygons
gamma AB DE CB FE two overlapping polygons
gamma+1 AB DE CB FE two overlapping polygons
gamma+2 AB CB DE FE two separate polygons
A simple ray-tracing algorithm can be used to find visible surfaces, as opposed to a more complicated algorithm that can be used to generate those o-so-pretty images.
Ray tracing is an image based algorithm. For every pixel in the image, a ray is cast from the center of projection through that pixel and into the scene. The colour of the pixel is set to the colour of the object that is first encountered.
Given a Center Of Projection
Given a window on the viewplane
for (each scan line)
for (each pixel on the scan line)
{
compute ray from COP through pixel
for (each object in scene)
if (object is intersected by ray
&& object is closer than previous intersection)
record (intersection point, object)
set pixel's colour to the colour of object at intersection point
}
So, given a ray (vector) and an object the key idea is computing if and if so where does the ray intersect the object.
the ray is represented by the vector from (Xo, Yo, Zo) at the COP, to (X1, Y1, Z1) at the center of the pixel. We can parameterize this vector by introducing t:
X
= Xo + t(X1 - Xo)
Y = Yo + t(Y1 - Yo)
Z = Zo + t(Z1 - Zo)
or
X = Xo + t(deltaX)
Y = Yo + t(deltaY)
Z = Zo + t(deltaZ)
t
equal to 0 represents the COP, t equal to 1 represents the pixel
t < 0 represents points behind the COP
t > 1 represents points on the other side of the view plane from the
COP
We want to find out what the value of t is where the ray intersects the object. This way we can take the smallest value of t that is in front of the COP as defining the location of the nearest object along that vector.
The problem is that this can take a lot of time, especially if there are lots of pixels and lots of objects.
The raytraced images in 'Toy Story' for example took at minimum 45 minutes and at most 20 hours for a single frame.
So minimizing the number of comparisons is critical.
- hierarchies of bounding boxes can be used where a successful intersection with a bounding box then leads to tests with several smaller bounding boxes within the larger bounding box.
- The space of the scene can be partitioned. These partitions are then treated like buckets in a hash table, and objects within each partition are assigned to that partition. Checks can then be made against this constant number of partitions first before going on to checking the objects themselves. These partitions could be equal sized volumes, or contain equal numbers of polygons.
From table 13.1 in the red book (15.3 in the white book) the relative performance of the various algorithms where smaller is better and the depth sort of a hundred polygons is set to be 1.
# of polygonal faces in the scene
Algorithm 100 250 60000
--------------------------------------------------
Depth Sort 1 10 507
z-buffer 54 54 54
scan line 5 21 100
Warnock 11 64 307
This table is somewhat bogus as z-buffer performance degrades as the number of polygonal faces increases.
To get a better sense of this, here are the number of polygons in the following models:
250
triangular polygons: 
550
triangular polygons: 
6,000
triangular polygons:
(parrot by Christina Vasilakis)

8,000
triangular polygons: 
10,000
triangular polygons:
(ARPA Integration testbed space by Jason Leigh, Andrew Johnson, Mike
Kelley)
Shading and Illumination