Lecture 5

Fundamental Algorithms (1 of 2)

(includes text and images from the 3rd edition of the VTK book)

Cells specify topology while points specify geometry

Types of Datasets (each of these has their own class in vtk) - a dataset has an organizing structure and a set of associated attribute data

Project 1 will start out with unstructured points and Project 2 will start out with image data, though in both cases the data may go through several forms depending on how it will be eventually be visualized

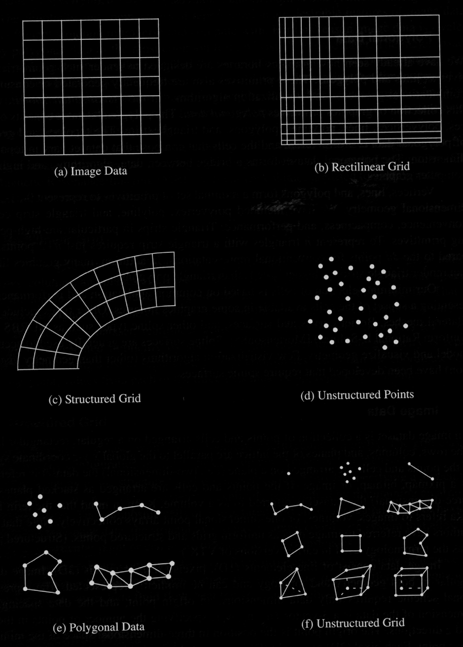
• image data - vtkImageData - points and cells on a regular rectangular lattice
  • if points and cells are arranged on a plane -> pixmap / bitmap / image
  • if arranged as stacked planes -> volume
  • regular (structured) geometry and topology
    
    
• rectilinear grid - vtkRectilinearGrid - points and cells on a regular lattice
  • rows, columns, planes are parallel to x-y-z coordinate system
  • regular topology, geometry only partially regular (spacing between points may vary)
    
    
• structured grid- vtkStructuredGrid
  • regular topology, irregular geometry
  • warped into any configuration w/o overlap or intersection
  • topology stored implicitely
  • geometry explicitely represented by array of point coordinates
  • cells are quadrilaterals (2D) or hexahedron (3D)
  • useful for finite difference computions - fluid flow, heat transfer, combustion
    
    
• unstructured points - vtkPolyData or vtkUnstructuredGrid - points irregularly located in space
  • no topology, completely unstructured geometry
  • typically converted to a more structured form for visualization
    
    
• polygonal data - vtkPolyData
  • unstructured topology and geometry
  • collection of graphics primitives (vertices, lines, polygons, triangle strips, etc)
    
    
• unstructured grid- vtkUnstructuredGrid
  • most general
  • completely unstructured topology and geometry
  • requires most memory and processing
  • used in structural design, vibration, dynamics, heat transfer

Cell

• type plus connectivity list (ordered list of point IDs) implicitely defines the topology
  

Linear Cells - linear or constant interpolation functions

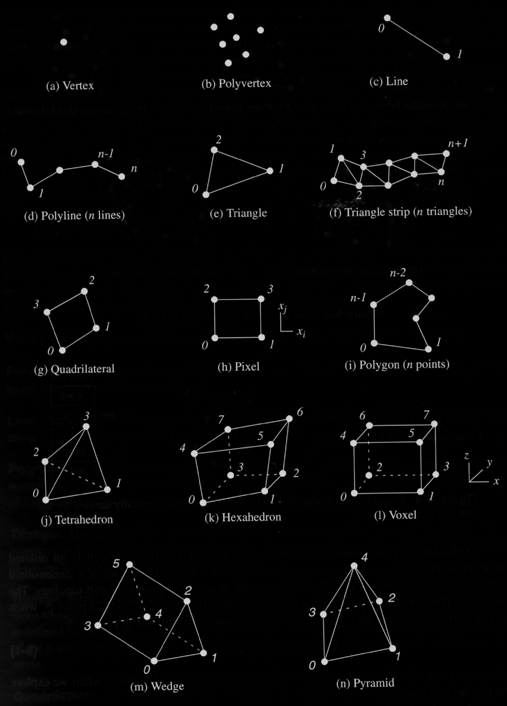
eg for the Hexahedron we can declare a cell to be a hexahedron and then give the connectivity list of point IDs (0, 1, 2, 3, 4, 5, 6, 7) where the point IDs in the connectivity list index into a (potentailly much larger) point coordinate list of x,y,z point locations. We know implicitely that 0,1 is one of the 12 edges and 0, 1, 2, 3 is one of the six faces.

• vertex - 0D cell
  • single point
• polyvertex - composite 0-dimensional cell
  • arbitrary ordered list of points

• line- 1D cell
  • 2 points - direction is from first to second
• polyline - composite 1-dimensional cell
  • one or more connected lines, from point i to i+1

• triangle - 2D cell
  • counter-clockwise ordering of 3 points
• triangle strip - composite 2-dimensional cell
  • one or more triangles, (i, i+1, i+2) defines a triangle strip
  • points need not lie in a plane
    
    
• quadrilateral - 2D cell
  • ordered list of 4 points in a plane,
  • counter-clockwise ordering, convex, edges do not intersect
    
    
• pixel* - 2D cell
  • special case of quadrilateral
  • ordered list of 4 points in a plane
  • each edge is parallel to one of the 3 coordinate axis (x, y, z)
  • each edge perpendicular to its adjacent ones
  • normal is parallel to one of the 3 coordinate axis (x, y, z)
  • points ordered in direction of increasing axis coordinate
  • note how this is not the same as a pixel on the screen
    
    
• polygon - 2D cell
  • ordered list of 3+ points lying in a plane
  • counter-clockwise ordering
  • may be concave, but not intersecting

• tetrahedron - 3D cell
  • 6 edges and 4 triangular faces defined by 4 non-planar points
• hexahedron - 3D cell
  • 12 edges and 6 quadrilateral faces defined by 8 vertices, convex
• voxel* - 3D cell
  • special case of hexahedron
  • 12 edges and 6 quadrilateral faces defined by 8 vertices, convex
  • each face is perpendicular to one of the axis
  • point list ordered in direction of increasing coordinate value
  • 8 'traditional' voxels form the corners of this kind of voxel
• wedge - 3D cell
  • 3 quadrilateral faces and 2 triangular and 9 edges defined by 6 vertices
  • must be convex, faces and edges must not intersect
  • ordered list of 6 vertices
• pyramid - 3D cell
  • 1 quadrilateral face and 4 triangular faces and 8 edges defined by 5 vertices
  • 4 points defining base must be convex, apex not coplanar w/ base

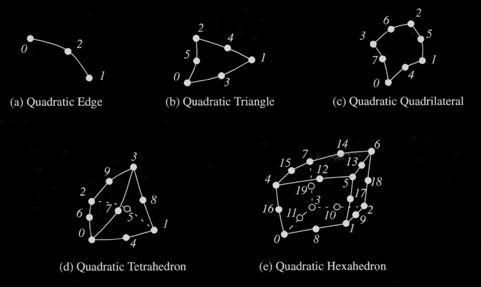
Nonlinear Cells

    more accurate rate interpolation functions
    model curved geometry better

linear cells are easily converted to linear graphics primitives. nonlinear cells (except maybe for NURBS) must first be converted (tesselated) into linear form

• quadratic edge - 3 points - 2 points at endpoints, 1 in middle of edge
• quadratic triangle - 6 points - 3 at endpoints, 3 in middle of edges
• quadratic quadrilateral - 8 points - 4 at vertices, 4 in middle of edges
• quadratic tetrahedron - 10 points - 4 at vertices, 6 in middle of edges
• quadratic hexahedron - 20 points - 8 at vertices, 12 in middle of edges

Attribute Data - each Cell has 0 or more pieces of attribute data associated with it.

• scalar - single value at each location in dataset (eg temperature)
  
• vector - magnitude and direction (eg wind speed and direction)
  
• normal - direction vector with magnitude = 1
  
• texture coordinate (2D, 3D) (eg a location in the visible human dataset)
  
• tensor (generalization of vector and matrix)
  • rank 0 - scalar
  • rank 1 - vector
  • rank 2 - matrix
  • rank 3 - 3D rectangular array

Categorize algorithms according to:

• structure - effect transform has on topology
• type - type of dataset the transform operates on

structure

• Geometric transformations - alter the geometry but not the topology
  • eg rotate or scale polygonal dataset
    
    
• Attribute transformations - convert data attributes to another form or create new attributes from input data
  • structure of dataset remains unaffected
  • eg compute vector magnitude
    
    
• Combined transformations - change dataset structure and attribute data
  • eg computing contour lines or surfaces
    
    
• Topological transformation - alters topology but not geometry or attribute data
  • eg converting polygonal data to unstructured grid
  • very uncommon

type

• scalar - operate on scalar data - eg generating contour lines from temperature on map
• vector - operate on vector data - eg showing oriented arrows of airflow on the same map
• tensor - operate on tensor matrices - eg showing components of stress using oriented icons
• modelling - generate topology or geometry, normals, texture data - vtk includes lots of misc algorithms in this category

Scalar Algorithms

single data value associated with each point in dataset

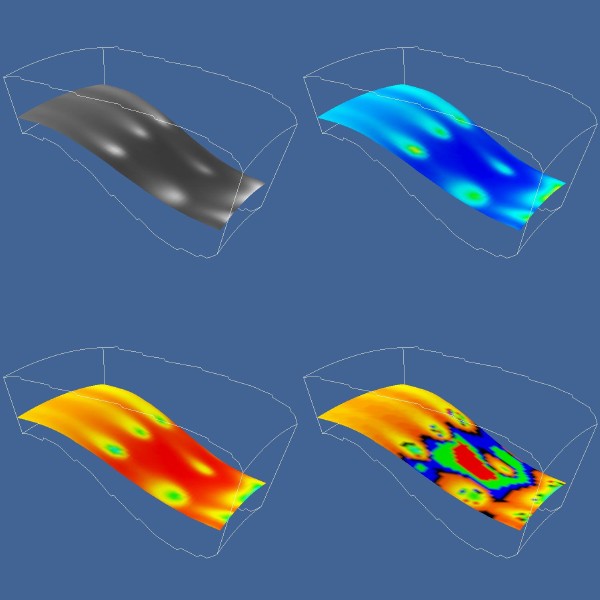
Flow density coloured with different lookup tables

• Color Mapping - map scalar data to colours using a discrete colour lookup table
  • lookup table holds an array of colours
    
  • lookup table has min and max scalar range
  • scalar values serve as indices into lookup table
    • if scalar > max then scalar = max
    • if scalar < min then scalar = min
    • map scalar value into the lookup table
  • transfer function - continuous mapping from scalar data to colour
  • mapping may be linear or logarithmic, etc
  • careful choice of colours is VERY important - Interaction of Color by Josef Albers
  • color brewer - http://colorbrewer2.org/ is a nice site to find good color combinations
    
  
  

  
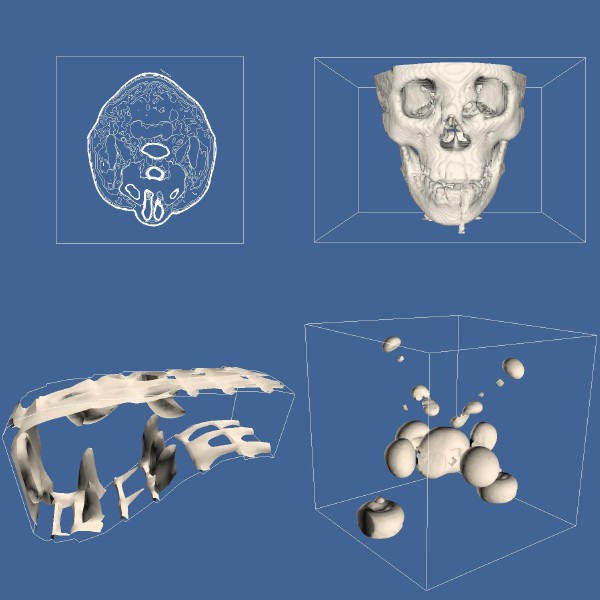
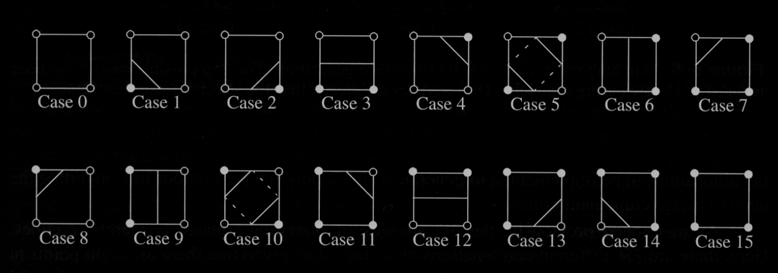
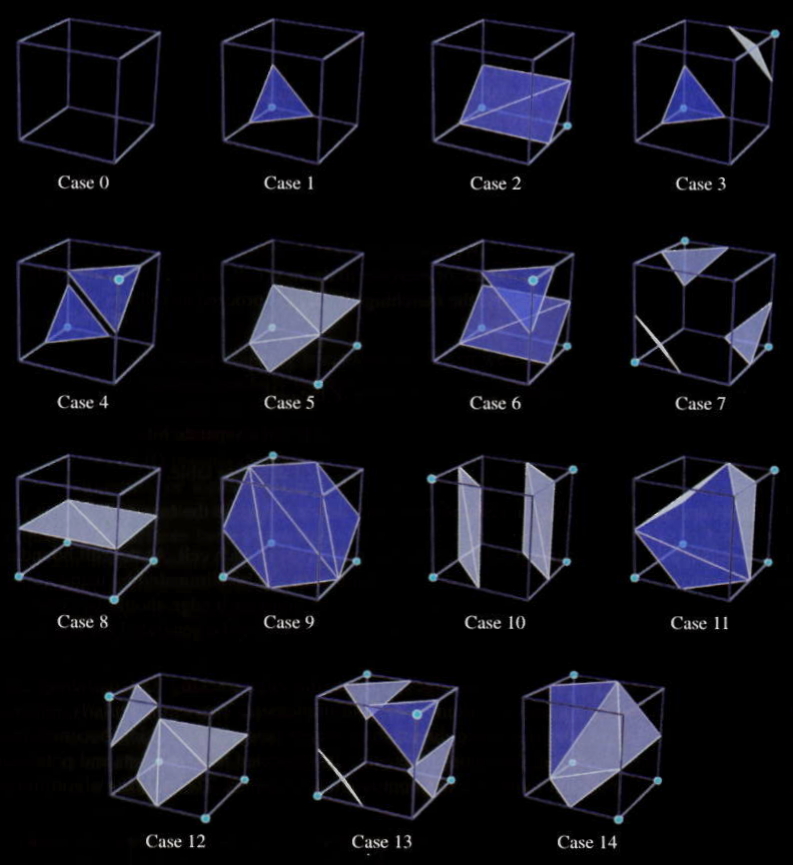
  Contouring examples. UL: Marching squares used to generate contour lines, UR marching cubes surface of human bone, BL marching cubes surface of flow density, BR Marching cubes surface of iron-proteint
  

• Contouring - constructing boundaries between regions
  • 2D - contour lines of constant scalar value
    • eg weather maps annotated with lines of constant temperature (isotherms)
    • eg topological maps with lines of constant elevation
  • 3D - isosurfaces - surfaces of constant scalar value
    • eg skin or bone in a medical image showing a constant intensity
  • generating contours probably requires interpolation between the given points
  • generate a new set of points then connect them into a contour

  • Marching Squares (2D) / Marching Cubes (3D)
    • assumes a contour can pass through a cell in only a finite number of ways
    • can create a table enumerating all these possible topological states of cell
      • # of states depends on # of cell vertices and # of possible in/out relationships
      • vertex is 'inside' if scalar value > value of contour line
      • vertex is 'outside' if scalar value < value of contour line
      • e.g. if cell has 4 vertices and each can be in or out then 16 possibilities
        • can represent these by a 4 bit code
      • currently not interested in 'where' the contour passes through cell, just 'how'
    • treats each cell independently
    1. select cell
    2. calculate inside/outside for each vertex of the cell
    3. create 4-bit index from in/out values
    4. use index to look up topological state
    5. interpolate contour location for each edge

    
    dark vertex is above the contour value, white vertex is below
    
    
    Here is a simple example where we generate a contour at value 5 by interpolating between the values in the cells.
    
    
    Moving to 3D things work pretty much the same
    
    

  • • may create duplicate vertices at cell boundaries to be merged later on
    • for marching cubes 256 possibilities for a cell with 8 vertices can reduce this to 15 using symmetry
    • contouring ambiguity in both 2D and 3D cases
      • may generate holes, or fill holes that should exist
      • more serious in 3D case
      • can add 6 more complementary cases to the 15

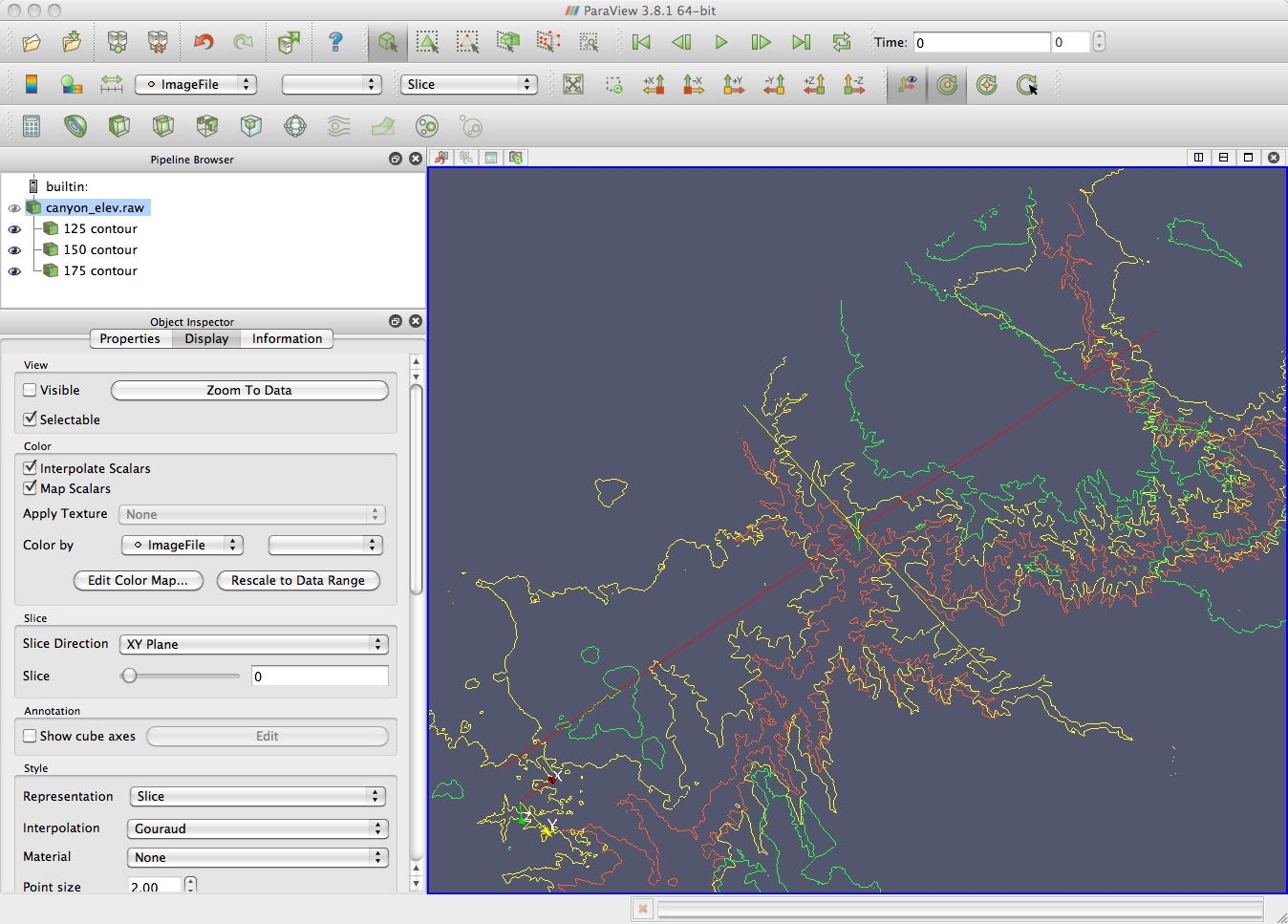
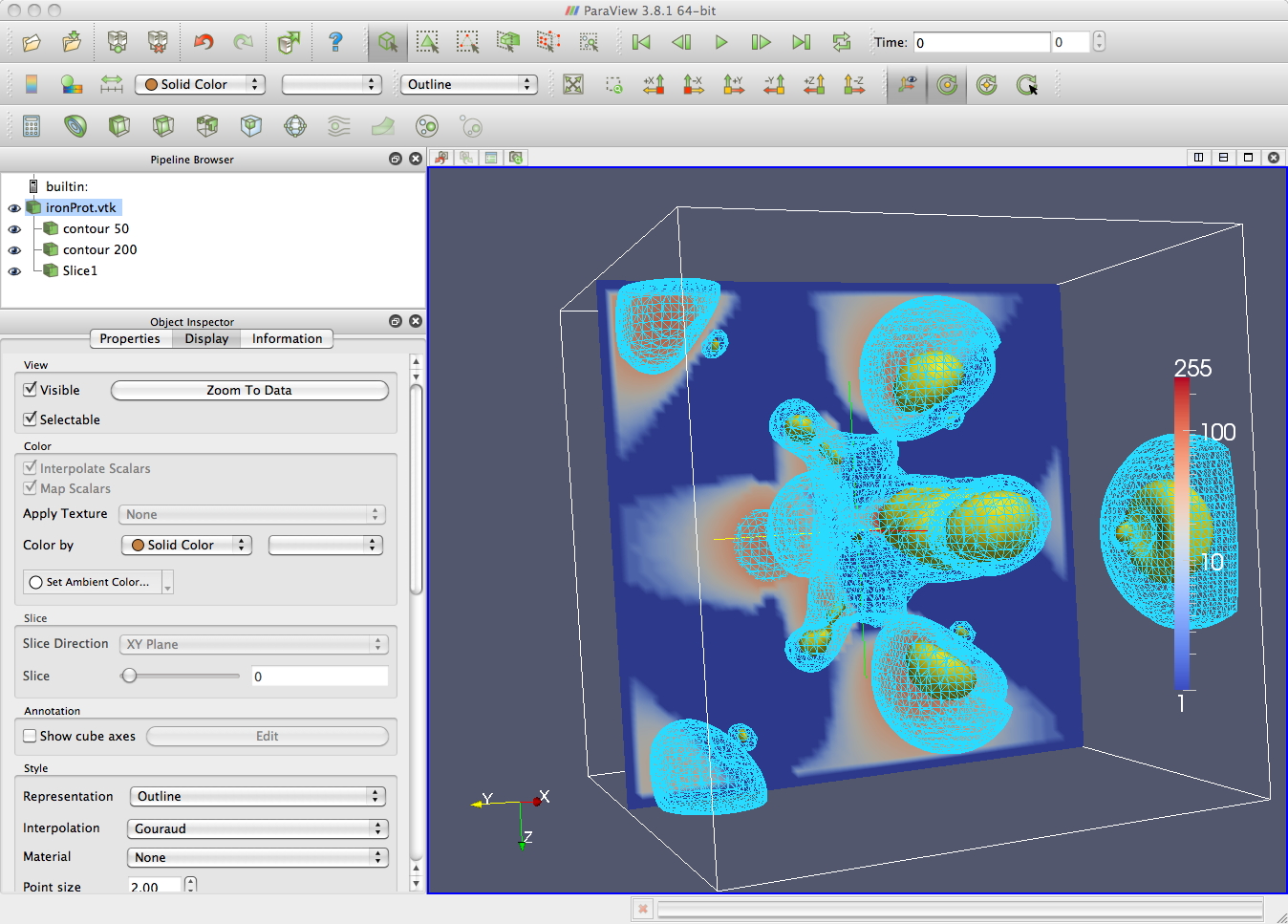
Some contours from last time - the grand canyon - 2D contours and Iron Protein - 3D contours

Vector Algorithms

• 3D representation of direction and magnitude
• Hedgehog - drawing an oriented scaled line for each vector
• Oriented Glyphs - 2D or 3D geometric representations can be used instead of lines
• Time Animation
  
• Streamlines - connect point positions over multiple timesteps
  • numerical approximation to a particle trace represented as a line
  • tracing trajectories in a vector field

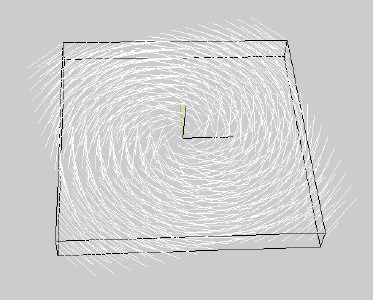
Three different representations of venctor data: hedgehog, glyphs, streamlines

• Warping - deforming geometry according to the vector field
• Displacement Plots - shows motion of an object in the direction perpendicular to its surface
  • motion is caused by applied vector field
  • vectors converted to scalars using surface normal (dot product) vector where + displacement is out from the surface and - into the surface
    

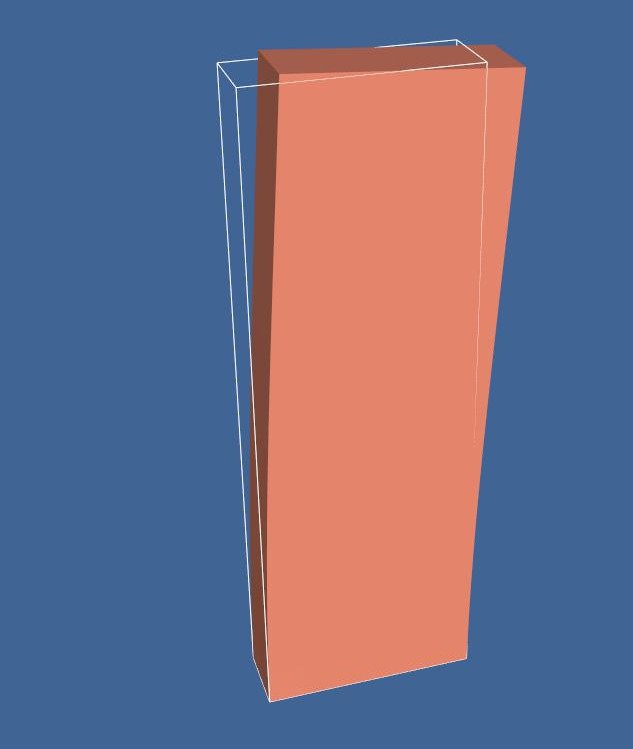warping

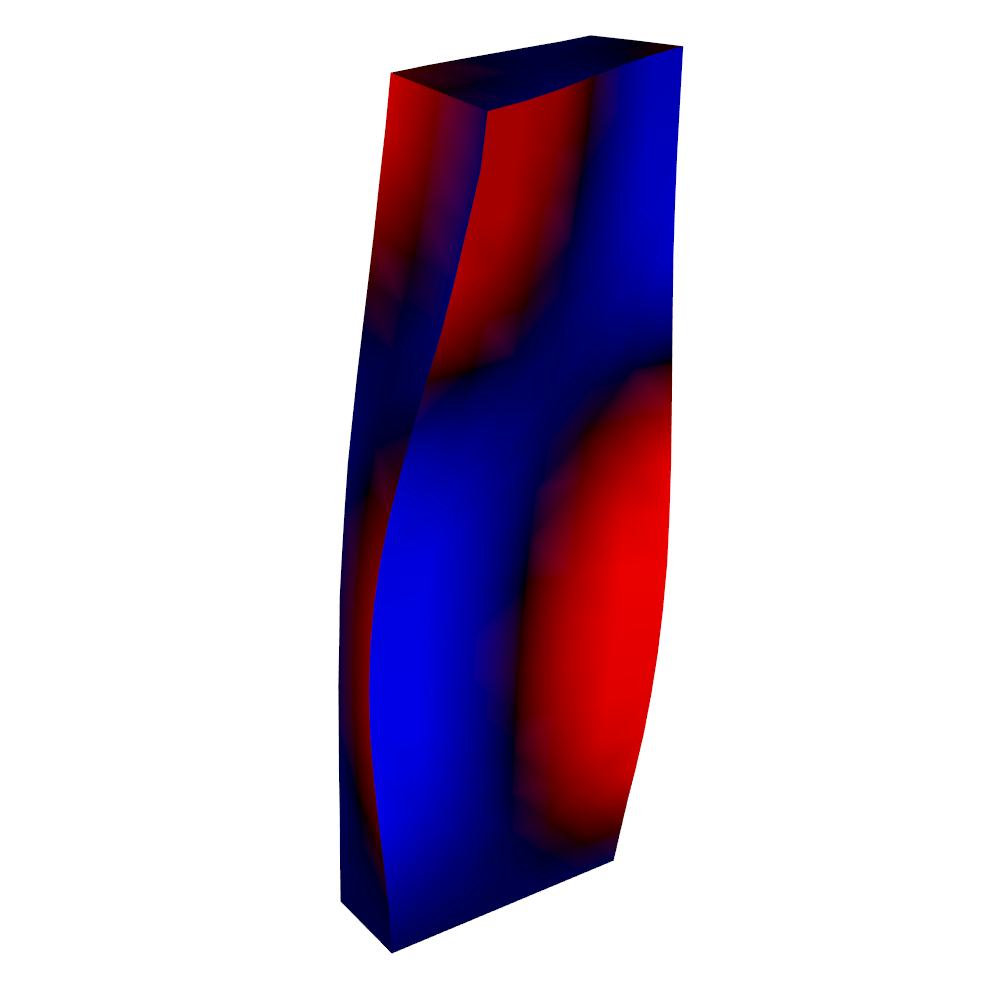displacement plot

and we previously looked at the grand canyon height map represented as a 2D texture which we warped on one axis into a 3D form and coloured based on its elevation

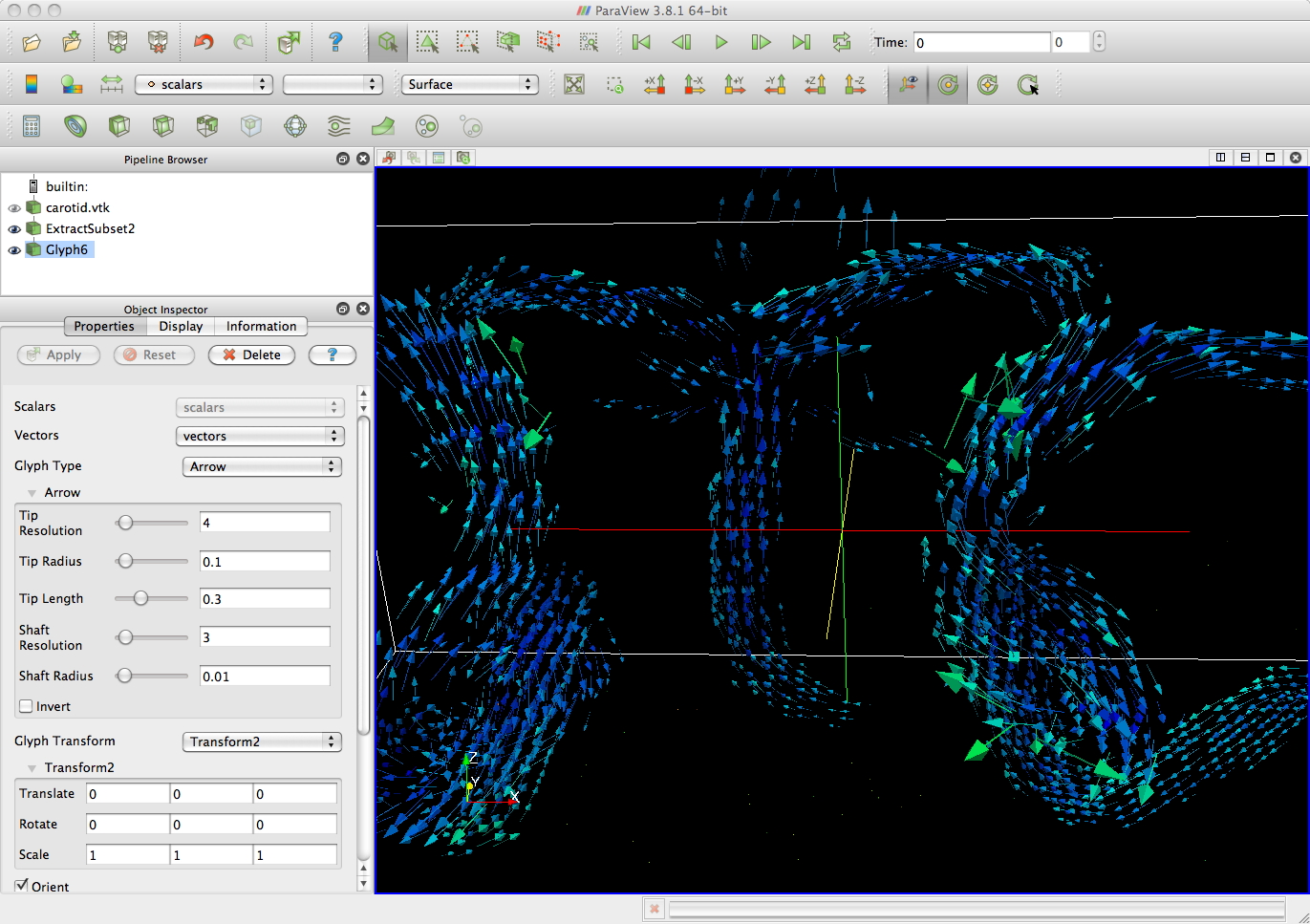
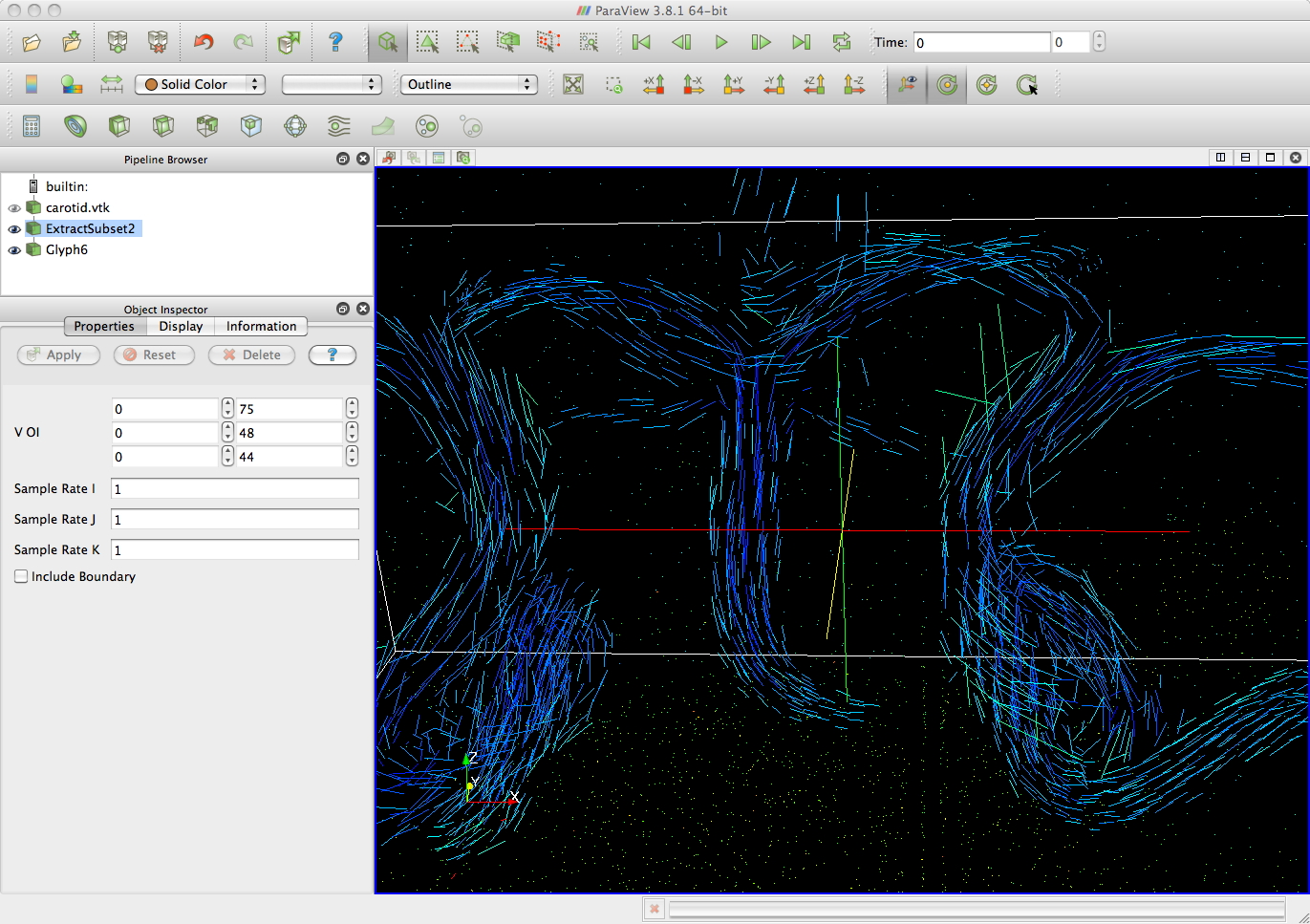
carotid.vtk from the textbook with 167,000 3D vectors shown as arrows, cones, and lines

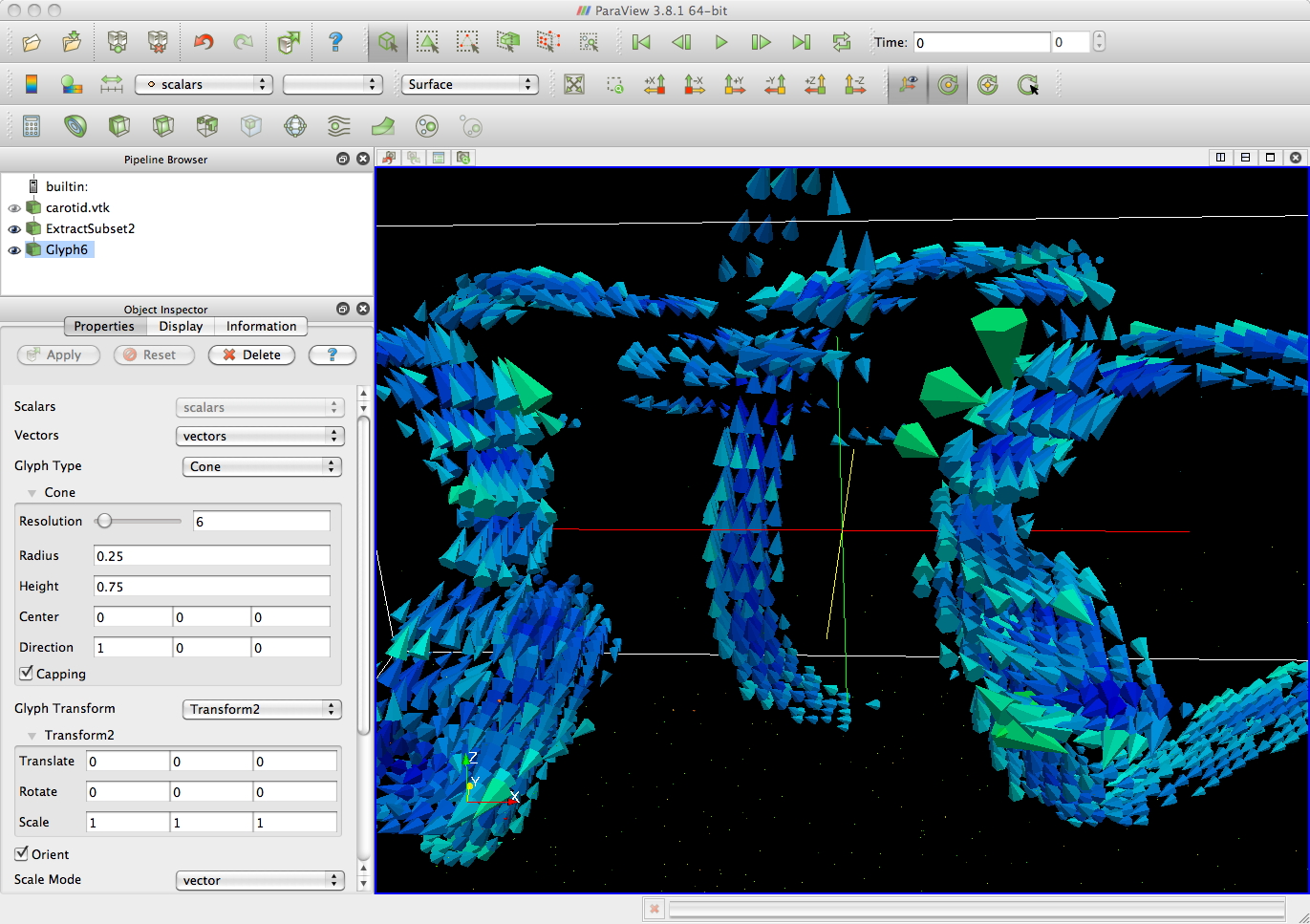
kithen.vtk from the textbook

first with glyphs - with complicated flow patterns it can be hard to see the flow from discrete vectors

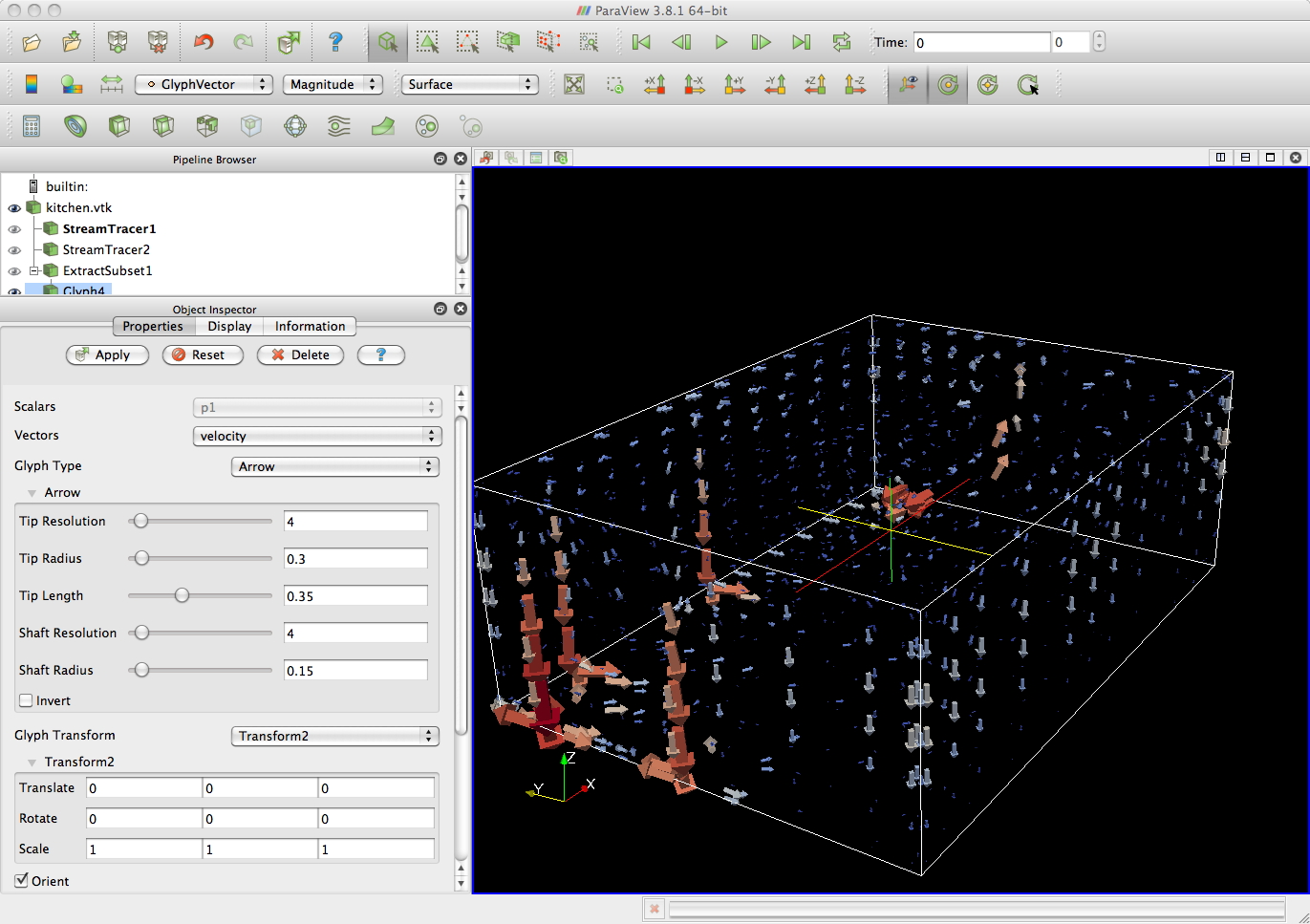
and then with 2 sets of streamtracers which integrate through the discrete vectors to show streams flowing from, to, or through a given set of points

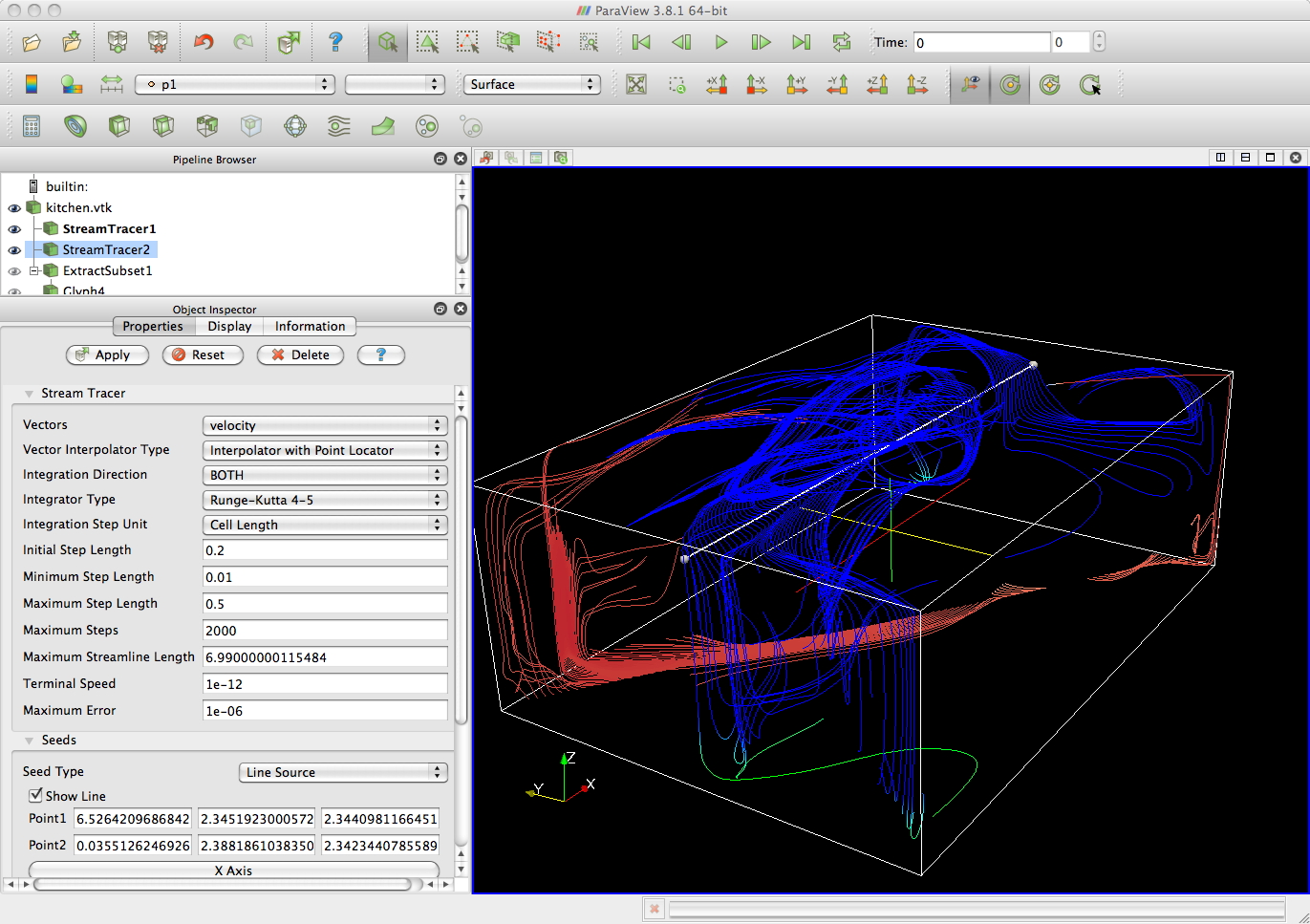
and streamlines starting from a particular area, with contextual polygonal information

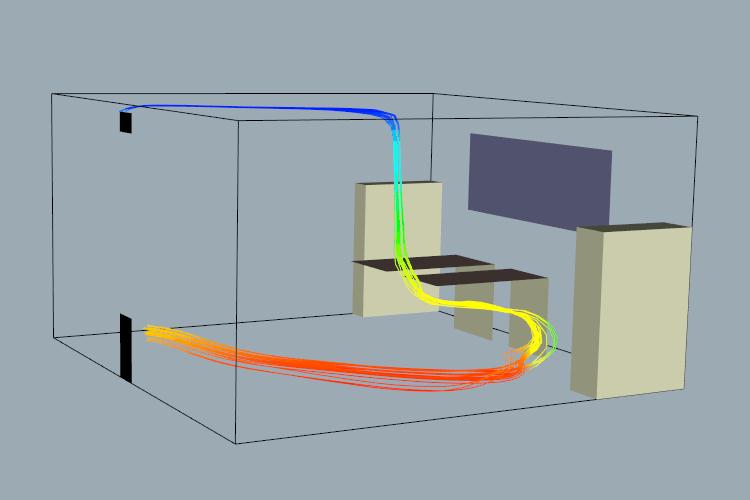
Coming Next Time

More Fundamental Algorithms