Lecture 6

Fundamental Algorithms (2 of 2)

(includes text and images from the 3rd edition of the VTK book)

Volume Rendering (Chapter 7 in Visualization Toolkit book)

Have data such as MRI or CT scans, ultrasound, etc

Direct Rendering (no intermediate geometric representation) vs Geometric Rendering

Image order vs object order

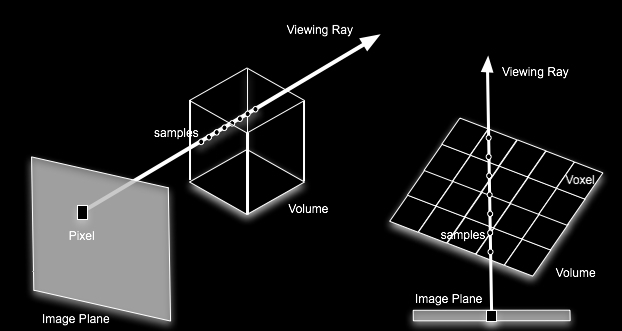
• image order - rays cast through each pixel in image plane through volume
• object order - volume traversed back-to-front (usually) processing each voxel
• hybrids

Image Order - raycasting / raytracing

• greyscale data values
  • minimum value = transparent black
  • maximum value = white
• determine values encountered along ray
• processing those values according to ray function - many possibilities
• volume is 3D image dataset w/ scalar values at points of a regular grid
• need an interpolation function to sample locations between the grid points
  • zero-order / constant / nearest neighbour returns closest grid point - simple
  • trilinear - linear interpolation between closest points along 3 axis
• can sample volume at uniform intervals while traversing the ray
  • need to take care in choosing step size - speed vs accuracy tradeoff
• or examine each voxel encountered while traversing the ray (fig 7-8)
  • convert the ray into a discrete form to obtain an ordered sequence of voxels
  • each voxel has 6 sides, 8 vertices, 12 edges
    • 6-connected if each share a face (best at finding small details)
    • 18-connected if share a face or an edge
    • 26-connected if share a face or an edge or a vertex (faster) (fig 7-10)
• ray: (x, y, z) = (xo, yo, zo) + (a, b, c) t where (a, b, c) is normalized direction vector

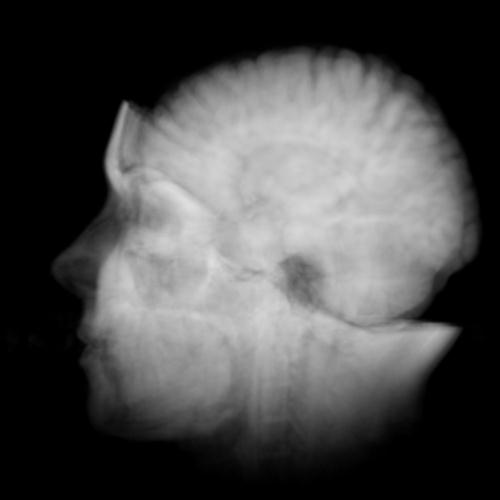
4 different ray functions - UL:maximum, UR:average, BL:distance=30, BR:composite

a nice program to explore this kind of data on the mac is osirix - http://www.osirix-viewer.com/

Object Order

• typically voxels traversed back to front or front to back and composited using alpha values
• similar to situation where everything in scene is a transparent polygon
• some algorithms do not need to process voxels in a particular order
• typically have triple nested loop:
  • for each plane ordered back to front
    • for each row of the plane
      • for each voxel in the row
        • determine its projected location on the view plane
        • alter the pixel at that location

• problem may occur in that by projecting back to the view plane we may have 'holes' as adjacent voxels may not map onto adjacent pixels
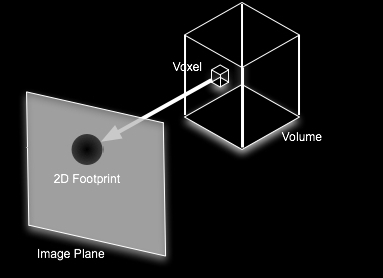
• solution is Splatting - distribute energy of voxel across multiple pixels in a splat/footprint
  • kernel with finite extent placed around each data sample
  • footprint is projection onto the view plane
  • in parallel projection with symmetric kernel the footprint is identical for all samples aside from its location so fast
  • type of kernel, radius of kernel, resolution of footprint table all affect results

• texture mapping volume rendering - based on hardware in the graphics cards/boards
  • 2D or 3D
  • project a set of texture mapped polygons which span the entire volume

  1. sampling step using interpolation (multiple methods, hardware/software)
  2. blending step to combine samples in the frame buffer

  

  Volume rendering using 2D (left) and 3D (right) techniques

  • 2D
    • dataset decomposed into orthographic slices along axis of volume most parallel to the viewing direction
    • move through slices back to front downloading 2D texture into memory, projected
    • may need to interpolate between slices
    • performance based on
      • software sampling rate
      • texture download rate
      • texture scan conversion rate
        
        
  • 3D
    • if enough texture memory, entire volume download into texture memory
    • series of planes parallel to view plane along viewing direction generated
    • polygons generated and projected back to front (fig 7-14)
    • 3D interpolation is done on the card/board
    • if not enough texture memory, break the dataset into subvolumes (bricks)
    • where each brick can fit in texture memory
    • process bricks back to front being careful of the boundaries

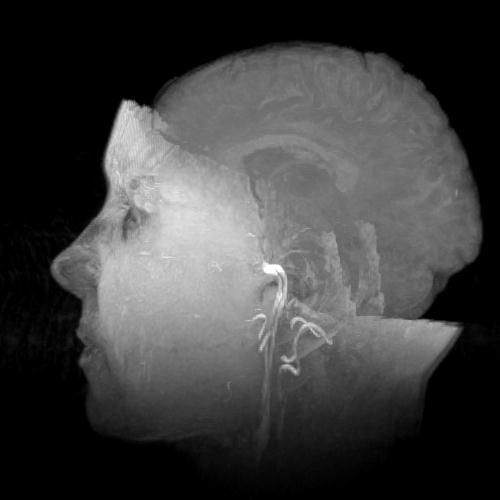
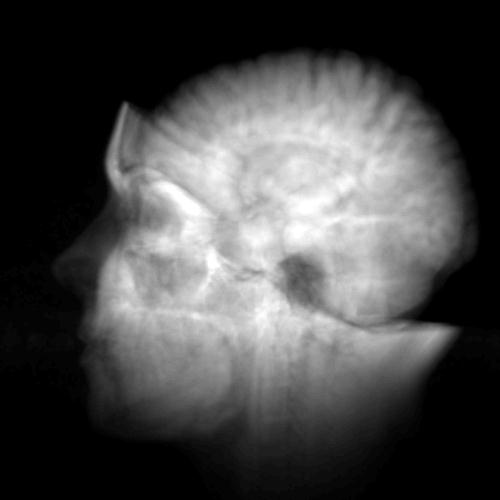
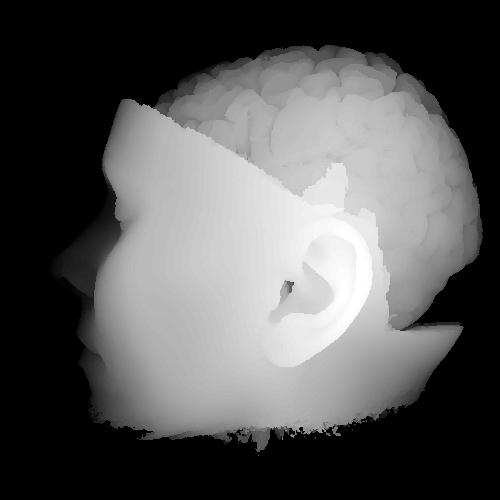
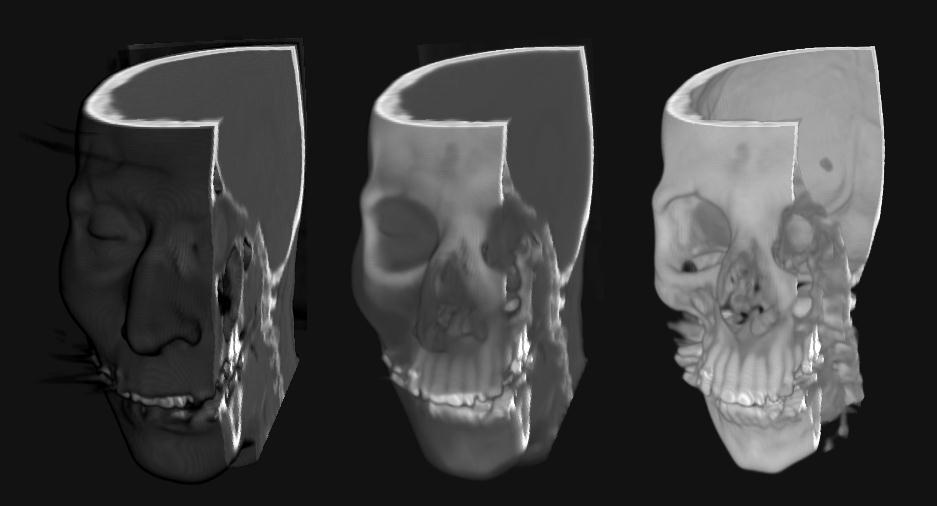2D Texture-mapped volume rendering with different opacity mappings

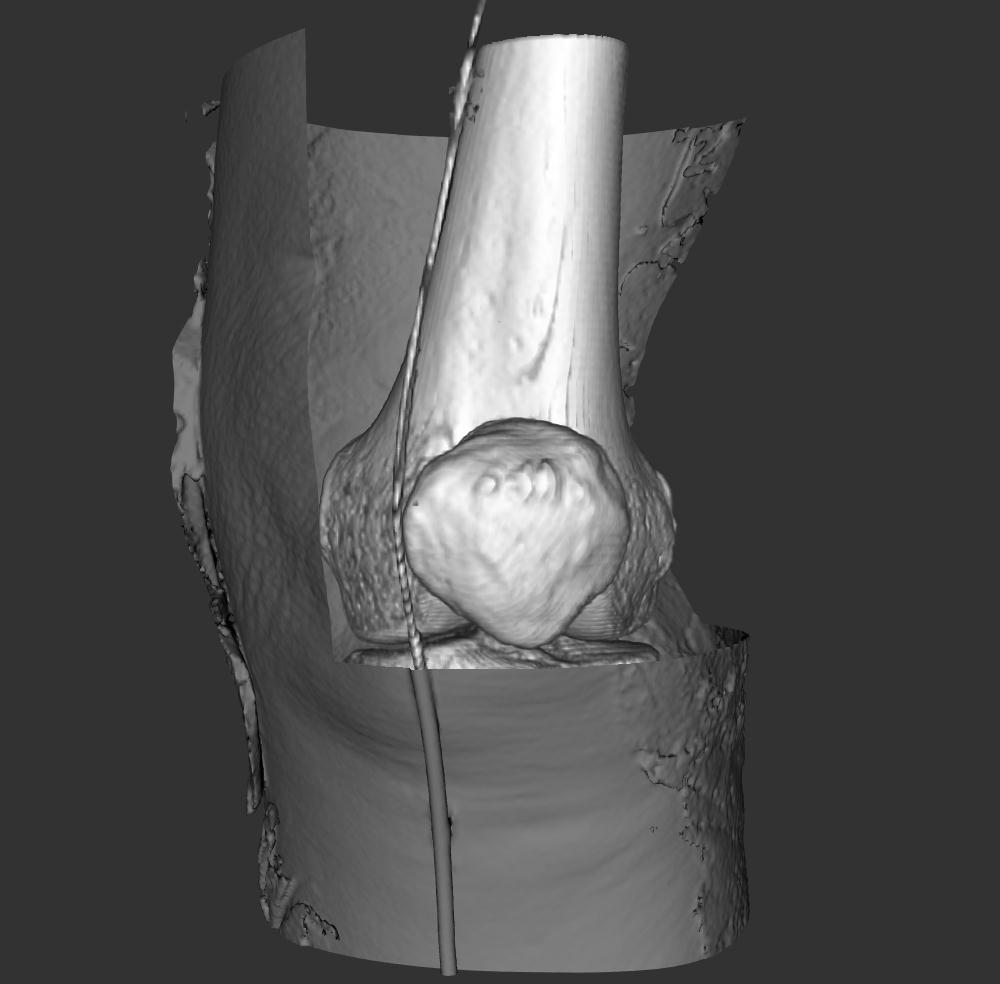
Volume Classification

• transfer function maps information at voxel location into material / colour / opacity
  • eg differentiating air, muscle, bone in a CT scan
• can have separate functions for red, green, blue, opacity

Regions of Interest

• often need to look through parts of the volume to see other parts of the volume
• can specify a partial region of the volume to render that contains interesting things
  • use clipping planes or other geometric forms to specify the region

create or change dataset topology or geometry

Source Objects

• Modelling simple geometry
  • generate sphere, cone, cube
    
  • read in model files with more complex geometry
    
    
• Supporting Geometry
  • additional geometry to support/enhance understanding of the visualization - here is code to create the office airflow visualization including very simple furniture http://web.cs.wpi.edu/~matt/courses/cs563/talks/vtk/office.html
    
    
• Data attribute creation
  • procedures to create data and attributes
  • for textures
  • for populating a grid with scalar values
    
    
    
    
  implicit functions F(x, y, z, etc) = c  eg for a sphere F(x, y, z) = x^2 + y^2 + z^2 - r^2 
  • properties:
    • simple geometric description
    • region separation (inside [ F<0], on [F=0], outside [F>0])
    • scalar generation to convert point in space into a scalar value
  • uses:
    • modelling objects
      • can sample F on a dataset and generate an isosurface at contour value c to get a polygonal representation of the function
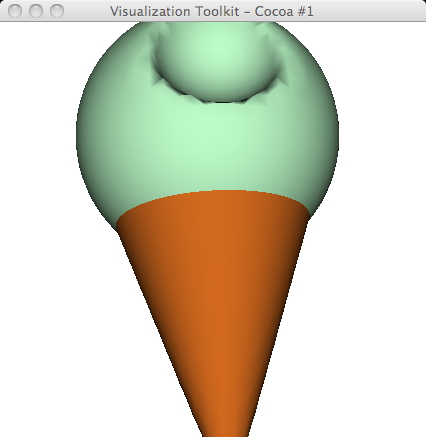
      • can perform boolean operations (union, intersection, difference) to create complex objects eg vtk ice cream cone in the Examples/Modelling directory
        
        
    • selecting data
      • can select or extract data by choosing cells, points within a particular region. Cell is within a region if all its points are within the region. Evaluate each point and check its sign
      • can perform boolean operations as with modelling
        
        
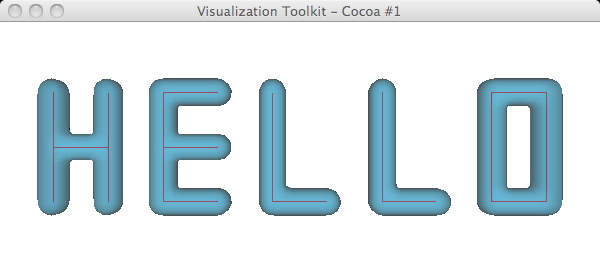
  implicit modelling
  • similar to modelling above except scalars generated using distance function rather than implicit function
  • distance function computed as Euclidean distance to set of generating primitives (point, line, polygon)
  • isosurface values are distances to generating primitive
  • can perform boolean operations
  • eg hello.tcl
  • some nice slides (with bad choices of color) on this here: http://www.cpsc.ucalgary.ca/~jungle/555/notes/implicit.pdf
    
    
  glyphs
  • object/icon that is affected by input data
  • may be geometry, image, dataset
  • may orient, scale, translate, deform etc in response to input data
    
    
  cutting
  • cut through a dataset with a surface & display interpolated data values on the surface
  • can view data on arbitrary surfaces
  • cutting surface defined by an implicit function
  • evaluate F(x, y, z) for each point of each cell in the dataset
  • if not all points + or - then surface passes through the cell
  • generate isosurface F(x, y, z) = 0
  • interpolate cut edges to get data attribute values
  • can make multiple cuts with different isovalues then show them with transparency back to front to do volume rendering

Tensor Algorithms (Chapter 6.4 in Visualization Toolkit book)

here are some web pages with info about tensors:

http://en.wikipedia.org/wiki/Tensor
http://mathworld.wolfram.com/Tensor.html

visualizing 3x3 real symmetric tensors

• describe state of displacement or stress in 3D material
• stress tensor - stress is measure of loading - force per unit area (N / m^2)
• strain tensor - strain is measure of displacement - change in length over length (dL / L)
  
  
• diagonal coefficients are normal stresses and strains
  • act perpendicular to a surface
  • normal stress is either compression or tension
• off-diagonal coefficients are shear stresses and strains
  • act tangentially to a surface
• 3x3 real symmetric matrix can be characterized by eigenvectors and eigenvalues
  • eigenvectors - 3 multually perpendicular vectors in 3D - principal axis
  • eigenvalues - 3 numbers
  • bunch of math to get eigenvalues and eigenvectors (http://www.sosmath.com/matrix/eigen0/eigen0.html or http://mathworld.wolfram.com/Eigenvalue.html)
• ordering the eigenvalues largest to smallest allows us to name the eigenvectors
  • major, medium, and minor in the same ordering
    
    
• visualization through tensor ellipsoids
  • position a sphere at tensor location
  • eigenvectors form axis (major, medium, minor) of an ellipsoid
  • eigenvalues used to scale the sphere/elipsoid
  • there is a vtk example at http://bluwiki.com/go/Visualize_Tensor_Field
    
• visualization through tensor axes 
• instead of ellipsoid, just show the principal axes

Coming Next Time

Visualization reports from the 00s - Part I