Lecture 7

Kinematics / Motion Tracking / People

images from http://www.animationartist.com

Sebastian Grassia's SIGGRAPH 95 Inverse Kinematics notes

Motion Tracking

latest iteration of rotoscoping

What do we want to capture

- facial movements - e.g. use a human actor to animate the facial features of a cat

- figure motion within a limited space - e.g. a person doing tai chi chuan

- figure motion within an extended space - e.g. small group playing basketball or fighting

Types of Tracking

• Optical
  • + reflective markers placed on body so no cabling, multiple videocameras at known locations
  • + large tracking space
  • - movement (especially with multiple actors) can occlude markers
  • - more expensive
  • - lighting conditions must be carefully controlled
• Magnetic
  • + no occlusion issues
  • + less expensive
  • - cabling
  • - can be affected by metal in the vicinity
  • - medium tracking space

Currently Optical is the most popular way of doing the work.

How many sensors are needed?

• The more points that are captured, the less the need for inverse kinematics
• 50 - 60 sensors per actor spread over the important areas
• Need to calibrate the cameras / sensors for the scenes to be shot

Talent?

• For specific actions use people who are used to doing those movements (e.g. athletes), for expressive movements use people who know how to move (dancers, actors)
• Actors can not do cartoon physics - the animators will need to augment the performance later
• Need appropraite props - instead of pretending you are holding a football or a big heavy gun, give the talent a football or a big heavy gun-shaped thing to hold - may need to track the prop as well

What to do after capturing the information?

• check to see if enough data collected (occluded sensors)
• deal wih noise - cleanup
• smoothing / interpolation
• deal with angle problems in the inverse kinematics
• enhancement (squash and stretch etc)

Current systems allow you to apply the character's motion to the CG character in real-time to see if everything is working correctly (or at least correctly enough that you can move on to the next shot

Motion Capture studios charge > $10,000 per hour

People in the backgrounds in Titanic, reissue of classic Star Wars

Secondary alien characters in Star Wars new trilogy

Main fantasy characters in Shrek, King Kong

Main human characters in Final Fantasy - the Spirits Within and Final Fantasy Advent Children

For Final Fantasy there was no facial motion capture

For capturing the action the set was 8 by 10 by 2.5 metres with 16 cameras

Some simple examples of motion capture in the CAVE using only two trackers.

Examples from King Kong (2005), and previously Walking with Dinosaurs had some nice examples.

In a couple weeks we will take a look at EVL's motion capture facility to get you ready to make use of it in the third project.

Kinematics

"The branch of mechanics concerned with the motions of objects without being concerned with the forces that cause the motion."

Forward Kinematics

Given a linked structure with joints and the angles at each joint, forward kinematics gives us the position at the end of the structure (end effector). There is a solution.

Unfortunately from an animation point of view we are often interested in giving a position for the end of the linked structure and having the joints realistically do what they need to do to accomplish that. For example animating a person reaching up to grab a particular book off a bookshelf, or bending down to pick up a book off the floor. This brings us to ...

Inverse Kinematics

goal directed motion

There may be 0, 1, or more solutions - i.e. if I want to grab a particular book on the shelf with my right hard, I might not be able to reach it from where I are currently standing no matter how I move my upper arm, lower arm and wrist, or there may be several different possible upper arm / lower arm / wrist orientations that satisfy my hand (end effector) grabbing the book.

overconstrined system - there is no solution
underconstrained system - many solutions

A lot of the research in this area comes from robotics - you have an articulated robot arm and you want it to grab the book on the shelf for you - how do you set all the appropriate joints to do that. Robots have particular types of joints; humans have particular types of joints, differet animals have different types of joints.

For one or two simple joints then there may be a small finite number of analytical solutions, but living creatures are much more complicated.

To model a human being correctly its important to understand the differing degrees of freedom in joints of human body

http://ovrt.nist.gov/projects/vrml/h-anim/jointInfo.html

Given the number of joints in the hands, they can be particularly complicated.  How about something a little simpler:

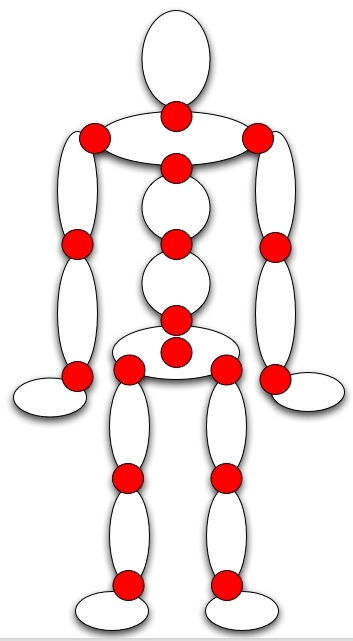
Its also important that the motion not only be possible but that it match the way humans move - ie if we have the choice of moving our hand or our entire arm we will minimize our effort and move just the hand. While a computer knows exactly where our hand will end up, human beings are constantly making adjustments so our movement wont be as smooth or predictable as that generated by a computer through simple interpolation.

Here are some samples from a nice set of slides by Bill Baxter at UNC on inverse kinematics

Basically what we want to do is incrementally solve the problem. At each time step we work out how to move/rotate each joint to move the end effector towards the goal. The simplification is that for a small enough time period the actual angular motion can be approximated by linear motion.

given a set of joint angles θ (θ₁, θ₂, θ₃, etc, and the end effector located at e_x, e_y, e_z then:
 e = f(θ) so given all of the θs we can compute e

what we want is that given e we can compute (a, the best) set of θs: θ = f^-1(e)

We are going to use the Jacobian which is a matrix of partial derivatives of all of the angles relative to the position of the end effector. In the more complicated case you would also deal with the rotation of the end effector and add rows into the Jacobian for the roll, pitch, and yaw of the end effector

Jacobian J = δ e / δ θ which can be expanded into this matrix

| δ e_x / δ θ₁     δ e_x / δ θ₂ ... δ e_x / δ θ_n |

| δ e_y / δ θ₁    δ e_y / δ θ₂ ... δ e_y / δ θ_n  | = J

| δ e_z / δ θ₁     δ e_z / δ θ₂ ... δ e_z / δ θ_n |

Its important that all of the values in the Jacobian are in the same coordinate system.

Each term in the matrix relates a change in that joint to a change in the end effector. Each column gives the change in velocity of the end effector relative to the change in a given joint angle.

So how do we compute the Jacobian? For a simple example lets say that the axis of rotation for these joints is going into the page and declare that p1 is at 0,0,0 then:

n_i = unit vector pointing out of the page
p_i = x,y,z location of joint i
V_i = e - p_i (the vector from p_i to e)
J_i (ith column) = n_i x V_i

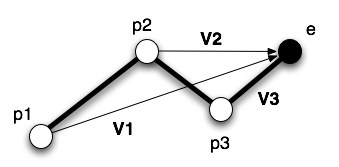
| ((0,0,1) X e)_x     (0,0,1) X (e - p2)_x    (0,0,1) X (e - p3)_x |

| ((0,0,1) X e)_y    (0,0,1) X (e - p2)_y     (0,0,1) X (e - p3)_y  | = J

| ((0,0,1) X e)_z     (0,0,1) X (e - p2)_z    (0,0,1) X (e - p3)_z |

Given the current location of the end effector, and the location we want the end effector to be at we can say:

Δ e = e_target - e_current
Δ θ = J^-1  Δ e
θ_t+1 = θ_t +  Δ θ

so we need to compute the inverse Jacobian (or a pseudo inverse if J is not invertable), and as long as Δ e is a small step the system will converge. If the step is too big the end effector may move away from the goal. Once the joint angles are changed then the Jacobian must be recomputed so the next time it is used the linear approximation will be accurate.

more on the jacobian at the ubiquitous wikipedia:
http://en.wikipedia.org/wiki/Jacobian

here are some more related notes:
http://freespace.virgin.net/hugo.elias/models/m_ik2.htm

Here is a simpler / faster algorithm called cyclic coordinate descent from A Hitchhiker's Guide to Virtual Reality by McMenemy and Ferguson

loopCounter = 0;
maxLoopCounter = some upper limit;

while (loopCounter < maxLoopCounter) and (target not reached)

    currentLink = last link in the chain (the pivot connected to the end effector)
    while (currentLink exists)
        {
        Rotate currentLink so that a line from currentLink through the end effector passes through the target
        // that will do the rotation all at once, for smoother motion
        // you probably want to define a max amount of rotation per iteration

        // Choose an axis of rotation that is perpendicular to the plane defined
        // by any two of the linkages meeting at the point of rotation.
        // Do not violate any angle restrictions

        currentLink = next link in the chain (away from the end effector)
        }

        loopCounter += 1;

Coming Next Time

flocking / artificial life

Lecture 7

Kinematics / Motion Tracking / People

Class has been cancelled today due to events on the East Coast.

Coming Next Time

more on kinematics / motion tracking / people