P02 - Distributed Painting with MPI
Late Policy
- Projects submitted late will incur a deduction of 10% per day, including weekends and university holidays, from the maximum possible score. Submissions beyond three days late will result in a score of 0. Each missing assignment will initially reduce your grade by 50 points [reflected as -50 points in Blackboard]. However, to mitigate this penalty, late submissions can be turned in for a grade of zero until the Monday of the final week of the semester, effectively removing the negative points.
Weekly Speedup Challenge
| Week | Results (speedup) | ||
|---|---|---|---|
| One (03/07) | 🥇 - | 🥈 - | 🥉 - |
| Two (03/14) | 🥇 Seyfal Sultanov - 21x | 🥈 - | 🥉 - |
| Three (03/21) | 🥇 Ali Siddiqui - 511x | 🥈 Seyfal Sultanov - 21x | 🥉 Kirk Tejas - 3x |
Distributed Painting with MPI
A Mandelbrot Set Parallelization Project
Overview
This project involves implementing a parallel version of the Mandelbrot set generation using MPI, focusing on efficiently leveraging multiple nodes to achieve significant performance improvements. It aims to explore how various node counts affect the computation speed and overall efficiency in a distributed computing environment.
Background: The Mandelbrot set is a complex and visually striking fractal that emerges from a simple iterative process applied to the numbers in the complex plane. The challenge lies in calculating whether each point on the plane belongs to the Mandelbrot set within a predetermined number of iterations.
Objectives
- Parallelize the Serial Code: Transform the provided serial code into a parallelized version utilizing MPI, focusing on effectively distributing the computation workload across multiple nodes.
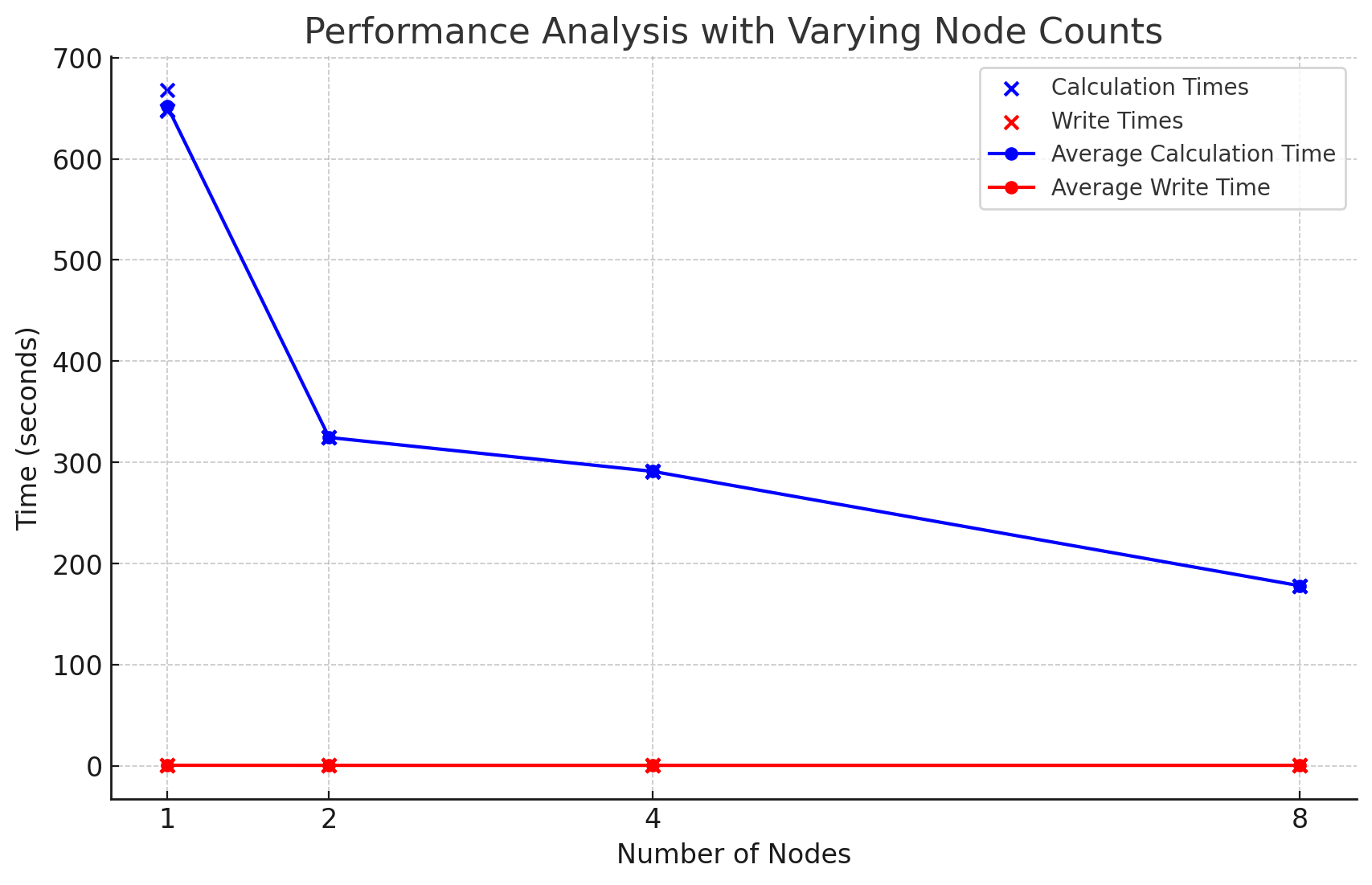
- Node-based Performance Scaling: Examine how performance scales when utilizing 1, 2, 4, and 8 nodes, with a constant iteration count of 10,000 and a minimum anti-aliasing sample rate of 4.
- Benchmark and Optimize: Aim to achieve the best performance on the extreme system, adhering to the edu_shared queue’s resource limitations. This involves measuring and optimizing the parallel code’s execution speed.
-
Speed-up Challenge: Compete in a speed-up challenge, submitting the most efficient results to earn extra credit. The base time for the speed-up calculation is 652.51s, the total time for image generation and writing to disk. Calculate speed-up with the equation:
\(\text{Speedup} = \frac{\text{Base Time}}{\text{Parallel Time}}\)
Where:- Base Time is 652.51s, the total time for serial execution. Parallel Time is the time it takes the parallelized version to generate and write the image to disk.
-
Final Submission Requirements:
- Performance Graph: This graph showcases the speed-up attained with various node counts, maintaining the iteration count at 10,000 and adhering to the anti-aliasing constraints. (mandelbrot-speedup.png)
- Source Code: Include the final parallel version that compiles and runs on the extreme cluster. (mandelbrot-mpi.cc and mandelbrot-serial.cc)
-
Makefile: Makefile builds mandelbrot-mpi for execution on extreme resources, has
make allandmake cleanwhere make all builds both mpi and serial versions, make clean removes executables, *.pnm, and *.png files. - Project Summary: Detail the MPI parallelization approach, challenges encountered, and insights gained. (mandelbrot.txt)
- PBS Script: Provide the PBS script used for job submission as part of the repository. (mandelbrot.PBS)
Extra Credit: Task-Based Parallelism (10 points)
Explore an advanced parallelization strategy by implementing a manager/worker model that distributes subtasks (sub-rectangles of the image) among worker nodes.
Requirements:
- Separate Implementation: This task-based solution should be distinct from the serial MPI implementation. (mandelbrot-task.cc)
- Performance Analysis: Include an additional graph comparing the performance of the task-based solution across 1, 2, 4, and 8 nodes. (mandelbrot-task-speedup.png)
- Approach Description: Briefly describe the manager/worker model, focusing on allocating and managing tasks across worker processes.
Grading Criteria
Grades will reflect the effectiveness and efficiency of parallelization efforts, focusing on the speed-up achieved and the innovation in the approach.
Ethics Statement
Encourage collaboration for learning, but ensure submissions are individual work. Cite any external sources or collaborators appropriately.
Submission Notes
Ensure the submitted code follows project specifications and semester-long guidelines, including the constant iteration count of 10,000 and the minimum anti-aliasing sample rate of 4. The goal is to optimize performance within these constraints while producing accurate and visually correct Mandelbrot set images.