
 |
nBody Simulation in CUDA- GPGPU Programming -Oct, 2008Sangyoon Lee (sjames @ evl.uic.edu)Electronic Visualization LaboratoryUniversity of Illinois at Chicago |
In project 2, we develope galaxy collision simulation with n-body interation algorithm. Milky way /Andromeda galaxy dataset is used (http://bima.astro.umd.edu/nemo/archive/#dubinski). In general, n-body simulation requires N square complexity of computation or N square memory space to reduce some of its computation (compute acceleration / velocity / position of bodies).
To achieve fast simulation, we utilize GPU's highly paralleled processing unit with CUDA. We especially focus on optimization of this simulation appropriate to GPU architecture and CUDA specifications.
Application developed and tested under Mac OSX 10.5 (Intel) with Nvidia Geforce 8600M GT chipset (macbook pro). Source code and binary is available below
galaxy: galaxy.tar.gz
Execution: just type ./bin/darwin/release/galaxy
Build: type make
* Requirements: to compile and execute appliction, you need to install nvidia CUDA driver / tools / SDK. (ver. 2.0). If you need more detials of this. See this link.
* Note: this application is the final version of the project. Therefore, performance will be the one mentionened in the last section. Application uses 8,192 bodies for simulation without approximation as default setup.
- Application Control
[Mouse control]
Rotate: Mouse left button and move
Zoom: Mouse right button and move
Pan: Mouse middle button and move
[Key control]
Reset scene: 'r'. reset simulation and camera to the initial state
Drawing type: 'd'. toggle between colored point / colored pointsprite / pointsprite (color represents the direction of current speed of particle. Red component to x-axis speed, Green component to y-axis, Blue component to z-axis)
Point Size: '+' / '-' to increase or decrease the size of point (point or pointsprite depends on current drawing mode)
First of all, we need to load inital dataset (Milky way/Andromeda). Given dataset includes 81,920 particles. Among those many particles, we only use disk and bulge of Milky way/Andromeda galaxy (total 49,152 particles. Exclude halo). This has 16,384 disk partcles and 8,192 bulge particles for each galaxies.
- Data Loader
When app initializes, it decides total number of particles simulation uses via app argument. Assume that this number is multiple of 4,096 to eliminate some complexity of parallel execution design of simulation. Data loader destribute this total number of particles evenly. For instance, if we simulate 8,192 particles, then half of it will be Milky way (4096 particles. 2730 for disk and 1366 for bulge) and another half will be Andromeda (4096 particles. 2730 for disk and 1366 for bulge). Following code snippet shows a data loading function.
void loadData(char* filename, int bodies)
{int skip = 49152 / bodies;}
FILE *fin;
if ((fin = fopen(filename, "r")))
{
char buf[MAXSTR];}
float v[7];
int idx = 0;
// allocate memory
gPos = (float*)malloc(sizeof(float)*bodies*4);
gVel = (float*)malloc(sizeof(float)*bodies*4);
int k=0;
for (int i=0; i< bodies; i++,k++)
{// depend on input size... skip lines}
for (int j=0; j < skip; j++,k++)
fgets (buf, MAXSTR, fin); // lead line
sscanf(buf, "%f %f %f %f %f %f %f", v+0, v+1, v+2, v+3, v+4, v+5, v+6);
// update index
idx = i * 4;
// position
gPos[idx+0] = v[1]*scaleFactor;
gPos[idx+1] = v[2]*scaleFactor;
gPos[idx+2] = v[3]*scaleFactor;
// mass
gPos[idx+3] = v[0]*massFactor;
// velocity
gVel[idx+0] = v[4]*velFactor;
gVel[idx+1] = v[5]*velFactor;
gVel[idx+2] = v[6]*velFactor;
gVel[idx+3] = 1.0f;
else
{printf("cannot find file...: %s\n", filename);}
exit(0);
- Particle Renderer
Once data loaded, app creates VBO and assigns initial value to it. Modified rendering routine in nvidia's n-body simulation is used to draw particles in three different mode. One colored gl point, the second one is colored pointsprite and the last one is pointsprite with predetermined color. You can toggle it via 'd' key. Also the size of point premitive can be changed interactively (refer to keyboard control section).
- Initial Screenshots (two types of pointsprites)
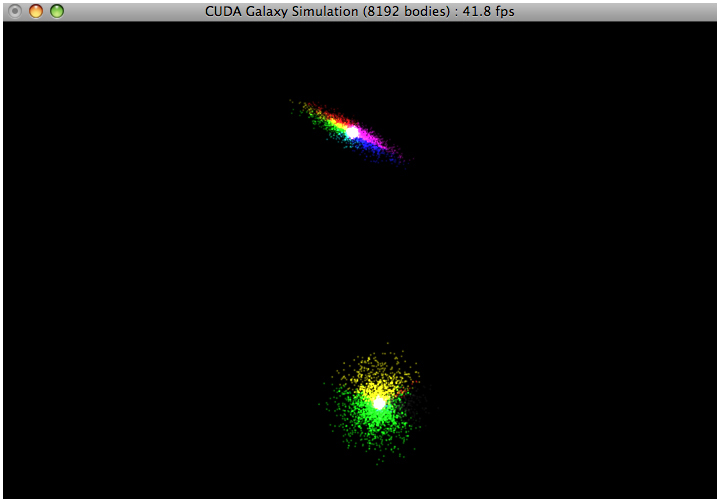
Now, we have all necessary data loaded. The next stage is to add computation code on CUDA kernel. Basic simulation code is grabbed from GPU Gems3 book chapter 31. As the first trial, algorithm does not consider any of performance issues here. All data (current position, mass & velocity) reside in device memory area (global memory). Each thread accesses all necessary data from this memory. With N loop, thread compute gravitation (acceleration) against all N bodies and accumulates and calculate new velocity and position.
This is naive N square algorithm and needs two N square read accesses to global memory (each thread read all N bodies' position and velocity values) and two N write access to it again (write out updated velocity and position). As expected, it is very slow. I only get 1.9 frames per second (8192 particles). With this low fps, it is almost impossible to check the simulation result (looks OK or something wrong with simulation parameters). Following code illustrates the CUDA kernel of this naive approach.
__global__ void galaxyKernel(float4* pos, float * pdata, float step, int bodies)
{// index for vertex (pos)
unsigned int x = blockIdx.x * blockDim.x + threadIdx.x;
unsigned int y = blockDim.x * gridDim.x + x;
// index for global memory
unsigned int posLoc = x * 4;
unsigned int velLoc = y * 4;
// position (last frame)
float px = pdata[posLoc + 0];
float py = pdata[posLoc + 1];
float pz = pdata[posLoc + 2]; // velocity (last frame)
float vx = pdata[velLoc + 0];
float vy = pdata[velLoc + 1];
float vz = pdata[velLoc + 2];
// update gravity (accumulation): naive big loop
float3 acc = {0.0f, 0.0f, 0.0f};
float3 r;
float distSqr, distCube, s;
unsigned int ni = 0;
for (int i = 0; i < bodies; i++)
{ni = i * 4;
r.x = pdata[ni + 0] - px;
r.y = pdata[ni + 1] - py;
r.z = pdata[ni + 2] - pz;
distSqr = r.x * r.x + r.y * r.y + r.z * r.z;
distSqr += softeningSquared;
float dist = sqrtf(distSqr);
distCube = dist * dist * dist;
s = pdata[ni + 3] / distCube;
acc.x += r.x * s;
acc.y += r.y * s;
acc.z += r.z * s;}
// update velocity with above acc
vx += acc.x * step;
vy += acc.y * step;
vz += acc.z * step;
// update position
px += vx * step;
py += vy * step;
pz += vz * step;
// thread synch
__syncthreads();
// update global memory with update value (position, velocity)
pdata[posLoc + 0] = px;
pdata[posLoc + 1] = py;
pdata[posLoc + 2] = pz;
pdata[velLoc + 0] = vx;
pdata[velLoc + 1] = vy;
pdata[velLoc + 2] = vz;
// update vertex position in vbo
pos[x] = make_float4(px, py, pz, 1.0f);
// update vertex color in vbo
pos[y] = make_float4(vx, vy, vz, 1.0f);}* Configuration Note: block has 1D 256 threads (256, 1, 1), grid has 1D 32 blocks (8192/256, 1, 1)
- Usage of float4 type
Above first kernel uses device memory type as float array (float*), one thing we've heard in class is that there is passible improvement when using float4 instead of float type. So, modified code to use float4* as device memory dataset. Then, application gets 3.1 fps. This is almost 50% increase. Guessing that when kernel access device memory, float4 type grabs all 4 float values at once while old code may read in float one by one. This also reduces some inteager instruction to compute array index within kernel code.
__global__ void galaxyKernel(float4* pos, float4 * pdata, float step, int offset)
{
...
// position (last frame)
float4 p = pdata[x];
// velocity (last frame)
float4 v = pdata[y];
...
for (int i = 0; i < bodies; i++)
{
r = pdata[i];}
r.x -= p.x;
r.y -= p.y;
r.z -= p.z;
...
...
// update global memory with update value (position, vel)
pdata[x] = p;
pdata[y] = v;
...}
In class, we have discussed about the approximation, which means that we may compute a part of bodies at each iteration (time step). For instance, one tenth of N bodies interaction per iteration. Since the first approach gives really bad fps, I decided to reduce some part of its iteration.
Here, I tested one sixteenth, one eighth, and one quater out of total N bodies. Sure, this gives much better performance. The reason is obvious. We reduced both computation and memory access time accordingly. Below code shows the changes in kernel code to accomodate this approximation. Parameter offset is controlled by application in the manner of modula increment (i.e. apprx = 16, then offset will be cycled from 0 to 15 as applicaton progresses.)
__global__ void galaxyKernel(float4* pos, float4 * pdata, float step, int offset, int apprx)
{...}
// consider sub compute chunk instead of whole N body
unsigned int start = (y - x) / apprx;
unsigned int end = start * offset + start;
start = start * offset;
for (int i = start; i < end; i++)
{// compute acceleration}
...
...Following table shows the change over three different approximation.
- Change in thread organization
Until now, I used a sort of extreme organization of thread/block/grid. After testing approximation, I tried to change this. Previously block(256,1,1), grid(32,1,1) used and new one is block(16, 16, 1) grid (16, 2, 1) it did not show any big difference at this point (16 was the magic number we saw in class). My guess is that the most serious bottleneck is too frequent global memory accesses.
So far, simulation only uses global memory and register. Great deal of performance gain expected is to utilize fast shared memory. Therefore, in this phase of optimization, kernel include shared memory access. Basic idea came from GPU Gems3 (use tile concept). Shared memory is only used to read in last frame data (position & velocity. two float4 per bodies). Kernel function is splited in similar way to CUDA example.
- Shared Memory Size?
Now, we need to think about how to organize shared memory. Simplest way would be to load all N bodies position into shared memory in the same block. This is another naive idea. But... total amount of shared memory per block limited to 16KB (Geforce 8600M GT). Let's do quick calculation to how much we need for each block. Most frequently used data is last position of bodies to compute acceleration.
8,192 bodies' position (float4) data size = 8,192 * 4 * 4 = 128 KB
Oops, this is too much. Cannot fit to the limitation. Also according to the CUDA programming guide (chapter 5.2), if there are multiple blocks running on the same multiprocessor, the total amount of shared memory used in single block must takes account for other blocks on the same processor. (i.e. two block per multiprocess, then at most half of shared memory use per block). Thefore, we need to cut this down somehow.
Nvidia's n-body example shows good example of how to split task as the manner of divide and conquer. So, I will use this concept to organize shared memory for each block.
Since shared memory is only visible to threads in the same block, each tile compute iteration is arranged in block base. Each block has 256 threads (16x16x1). In main kernel, each thread read single position & velocity data from device memory to shared memory (single iteration within block). Then, compute acceleration for this tile. This single iteration will repeat until it gets to the required number of body interaction (i.e. 8192 bodies in no approximation case. this is 32 iterations.). Following table shows comparasion of memory access pattern between old and new approaches.
Total bodies N: 8192, No approximation. Data type is float4. Table does not include VBO updates (same for both case).
Access Type read in (global) write shared mem read shared mem write out (global) Phase III N * N * 2 = 128 M
0 0 2 * N (pos & vel) = 16 K
Phase IV N * (N/256) * 2 = 512 K N * (N/256) * 2 = 512 K N * N * 2 = 128 M 2 * N (pos & vel) = 16 K * K and M means times not byte nor bit. (K = 210 times, M = 220 times)
As we can see in above table, new approach moves major memory read accesses to shared memory side. Another consideration is "Loop Unrolling". As GPU Gems3 indicates, there is a slight possible performance gain by unrolling loop. During computation of acceleration, each thread run through 256 bodies interaction for each tile. So, we surely can unroll some of it. Then, how much performance increses?
Table shows great performance improvements over utilization of shared memory. Loop unrolling (8 loop unroll) also gives us about 5 ~ 7% speedup. For the loop unrolling I used nvcc compiler directive, #pragma unroll (CUDA programming Guide pp.25). When I tried different number of loop unrolling more than 8, it did not give that much of improvements.
Here is the kernel code used for this testing. This is almost the final version of my n-body simulation.
__device__ float3 bodyBodyInteraction(float4 bi, float4 bj, float3 ai)
{
float3 r;
r.x = bj.x - bi.x;
r.y = bj.y - bi.y;
r.z = bj.z - bi.z;
float distSqr = r.x * r.x + r.y * r.y + r.z * r.z;
distSqr += softeningSquared;
float dist = sqrtf(distSqr);
float distCube = dist * dist * dist;
float s = bi.w / distCube;
ai.x += r.x * s;
ai.y += r.y * s;
ai.z += r.z * s;
return ai;
}
__device__ float3 tile_calculation(float4 myPosition, float3 acc)
{
extern __shared__ float4 shPosition[];
#pragma unroll 8
for (unsigned int i = 0; i < BSIZE; i++)
{
acc = bodyBodyInteraction(myPosition, shPosition[i], acc);
}
return acc;
}
__global__ void galaxyKernel(float4* pos, float4 * pdata, unsigned int width,
unsigned int height, float step, int apprx, int offset)
{
// shared memory
extern __shared__ float4 shPosition[];
// index of my body
unsigned int x = blockIdx.x * blockDim.x + threadIdx.x;
unsigned int y = blockIdx.y * blockDim.y + threadIdx.y;
unsigned int pLoc = y * width + x;
unsigned int vLoc = width * height + pLoc;
// starting index of position array
unsigned int start = ( (width * height) / apprx ) * offset;
float4 myPosition = pdata[pLoc];
float4 myVelocity = pdata[vLoc];
float3 acc = {0.0f, 0.0f, 0.0f};
unsigned int idx = 0;
unsigned int loop = ((width * height) / apprx ) / BSIZE;
for (int i = 0; i < loop; i++)
{
idx = threadIdx.y * blockDim.x + threadIdx.x;
shPosition[idx] = pdata[idx + start + BSIZE * i];
__syncthreads();
acc = tile_calculation(myPosition, acc);
__syncthreads();
}
// update velocity with above acc
myVelocity.x += acc.x * step;
myVelocity.y += acc.y * step;
myVelocity.z += acc.z * step;
myVelocity.x *= damping;
myVelocity.y *= damping;
myVelocity.z *= damping;
// update position
myPosition.x += myVelocity.x * step;
myPosition.y += myVelocity.y * step;
myPosition.z += myVelocity.z * step;
__syncthreads();
// update device memory
pdata[pLoc] = myPosition;
pdata[vLoc] = myVelocity;
// update vbo
pos[pLoc] = make_float4(myPosition.x, myPosition.y, myPosition.z, 1.0f);
pos[vLoc] = myVelocity;
}In tile_calculation function, shared memory access by all threads has the same memory address. This can be done as fast as register reading (refer to Dr. Dobb's tutorial. part 5.1). I think that this is the broadcasting feature of shared memory (refer to CUDA programming Guide, pp.62). One thing I was not sure is that document mentioned broadcasting occurs within 32bit word. My guess here is that float4 devided into 4 separate reads and each is 32bit word (guess based on double type example in CUDA programming Guide, pp.61). Therefore, above code can obtain fast access to shared memory.
The other consideration of memory optimization is access pattern of global memory access. According to Nvidia's n-body simulation kernel, it enforces each block not to read the same addresses when reading in data from global mem to shared mem. I was not sure if this is possible benefit or not. So, I tried it but did not get any big difference in performance. This was a bit strange.
We have seen a several techniques to improve n-body simulation so far. Most of all, shared memory utilization was best bet for the performance gain. According to Nvidia's implementation, there are a few more possible optimizations. Without getting too complex, phase IV reached almost 86% of nvidia example code in terms of performance (nvidia implementation showed 25.5 frames per second with 8,192 bodies without approximation).
Here are some comparision charts for summary.
First of all, finding simulation parameters was not easy at all. Even the final version of my work looks OK but not close to what I saw in class. Some of the parameters I played with are scale factor for each initial position, velocity and mass. In addition to this data scales, there were simulation timestep, softening of distance square, damping of velocity, and gravity constant. So, total 7 parameters play with... Not easy to find magic number for all even though I tend to fix total number of bodies.
Frequent global memory (device memory) access is really really bad in general. Shared memory is so cool and fast. Anyone who is thinking of CUDA app development must consider memory utilization very carefully to get the best performance.
Good material for memory architecture and optimization strategy is found in chapter 5.1.2 memory bandwidth in CUDA Programming Guide 2.0.
- Fast N-Body Simulation with CUDa, GPU Gems3, Chapter 31, Addison Wiesley, 2007
- N-Body simulation, Nvidia CUDA 2.0 SDK sample project, http://www.nvidia.com/object/cuda_get.html
- N-Body Data Archive, http://bima.astro.umd.edu/nemo/archive/#dubinski
- Performance Guidelines, Chapter 5, Nvidia CUDA Programming Guide 2.0, http://www.nvidia.com/object/cuda_develop.html