Begin the Quaternion Julia Sets Tour
|
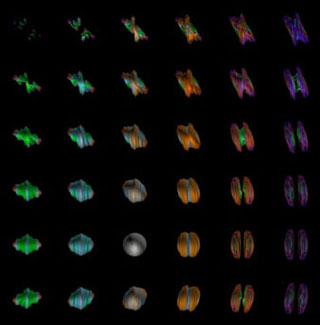
This array of images is designed to explore the quaternionic Julia sets, utilizing high-quality ray-traced images.
Each image is specified by three numbers, an angle and two real numbers.
One of the real numbers is called R, the other I, to denote the real and imaginary parts of the complex number R+Ii where i is the square root of minus one.
The complex number R+Ii can be regarded as a point in the plane, and we call this plane the constant space for the images.
The color
is a function of the distance from the origin to the point displayed.
The tour begins with the angle equal to zero and allows step-wise changes in the real and imaginary parts.
Choice of other angles is available, as well, once the tour has begun.
The area covered in the constant space for each angle is 4x4 units. The center of this area varies
from angle to angle to cover the most interesting Julia sets. The images are spaced by .25 units.
Each image of the quaternionic Julia set represents a 2x2 unit space at the origin.
Once inside the tour, click on each image to investigate the quaternion in greater detail.
|

