This page is a documentation of the Quaternion
Julia Sets in Virtual Reality project for SUPERCOMPUTING '95. I worked
on this project in collaboration with
Daniel J. Sandin, also of EVL, and
Louis H. Kauffman and
Yumei Dang, of the Department of
Mathematics, Statistics, and Computer Science at the University of
Illinois at Chicago.
what they are
A Julia Set is the map of the behavior of an equation when its output is
fed back into its input (recursive). The equation mapped is z=z**2+k.
In general, the most common Julia Set is a map of that equation in
complex numbers (2D numbers). In this case the equation is being mapped
in quaternions, which are 4D hyper-complex numbers. This project
investigates a method for visualizing Julia Sets based on estimating the
distance from the viewpoint to the surface of the Julia Set.
Here are some example images:




(larger version)
for more images, check out
Yumei's page.
in the CAVE
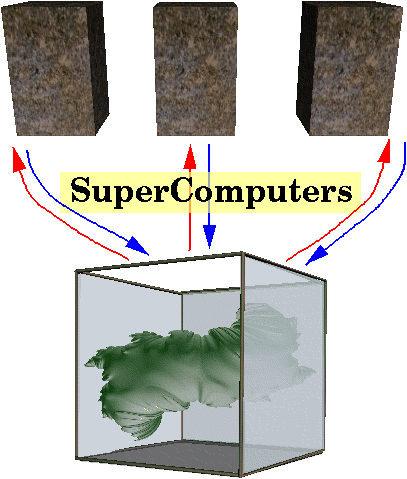
Because the process of rendering these forms is so computationally
heavy, there was a need to use as much computational power as was
possible. My primary contribution to this project was to supply this
power. To do this I used the CAVEcomm library developed at the
Mathematics and Computer Science Division of Argonne National
Laboratory to communicate between the onyx that runs the CAVE and three
seperate supercomputers that did all the calculations.
Even with three supercomputers working on ray tracing the Julia Set,
displaying it in real time is impossible. In order to eleviate the
problem of having nothing to look at while all this computation was
going on, we successively refined the image. This meant first ray
tracing the set in low resolution and displaying it on the walls of the
CAVE. We could then use the information from the low resolution image
to determine which areas had the most contrast. Those areas could then
be refined first, as they tend to be more interesting.
It was my responsability to establish the connections between the CAVE
and the supercomputers, and keep track of all the information that was
being sent back and forth. I received the pertinent data that would be
needed to do the calculations from the CAVE. That data was then sent to
which ever of the three supercomputers was least busy. The
supercomputer would calculate the appropriate section of the image based
on the information it received, and send the result back. I took those
results and gave them back to the CAVE, which displayed it in the
appropriate position.
back to NOW
back to
insley on the internet