Back to Loomis 205
... we begin with the original Loomis 205
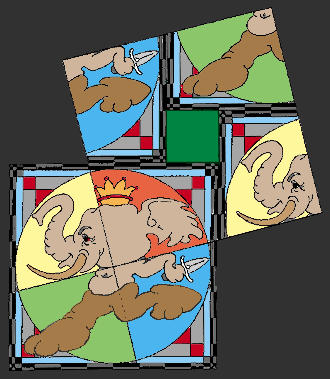
... by lifting the hypotenuse square up
...and out of the base square
...we are able to form the right-triangle [in yellow]
and riser square of Loomis 9.
(...the riser and the "captured" squares are of equal area [shown in green].)

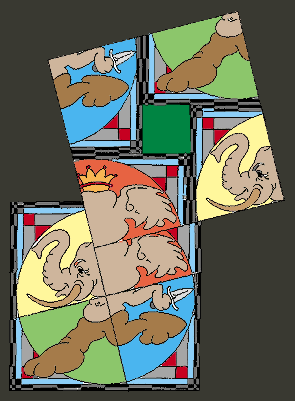
...and out of the base square

...we are able to form the right-triangle [in yellow]
and riser square of Loomis 9.
(...the riser and the "captured" squares are of equal area [shown in green].)
(...the riser and the "captured" squares are of equal area [shown in green].)
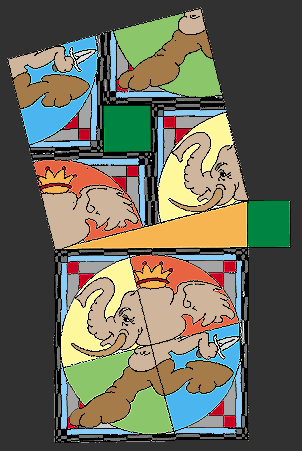
This picture clearly shows that the hypotenuse square
has been formed by cutting and inverting the base square.
[...the consturction of Loomis 9.]
(...note that the outer corners of the base square are all tucked into
the center to construct the hypotenuse with its "captured"[green] area.)
This concludes our look into the Pythgorean Proposition.

