Chinese Proof

Loomis 91

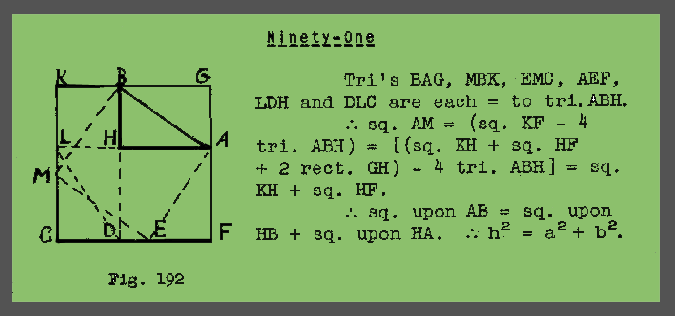
Part II, Proof 91, page 154 from E.S.Loomis, The Pythagorean Proposition (1940)

The Chinese Proof in Four Parts

This ingenious proof (found in an ancient Chinese text) begins with two equal area squares, the hypotenuse square at the top, and the base square below.

All the elements of the proof appear as the animation begins. Four congruent triangles surround the hypotenuse square, and four others around the riser and base squares.

As the hypotenuse square rotates, it also shrinks in size as the riser square grows and the base square shrinks. These expansions and concractions maintain the equal area within the bounding squares.

The triangles have increased their angles to fourty-five degrees,ie., to half a sqaure. The base and riser squares are equal to each other, and with their four triangles, they are equal in area to the hypotenuse square and its four surrounding triangles.