The intrinsic geometry of the human brain connectome
October 22nd, 2015
Categories: Applications, Virtual Medicine, VR, Visual Analytics
Authors
Ye, A. Q., Ajilore, O. A., Conte, G., GadElkarim, J., Thomas-Ramos, G., Zhan, L., Yang, S., Kumar, A., Magin, R. L., Forbes, A. G., Leow, A. D.About
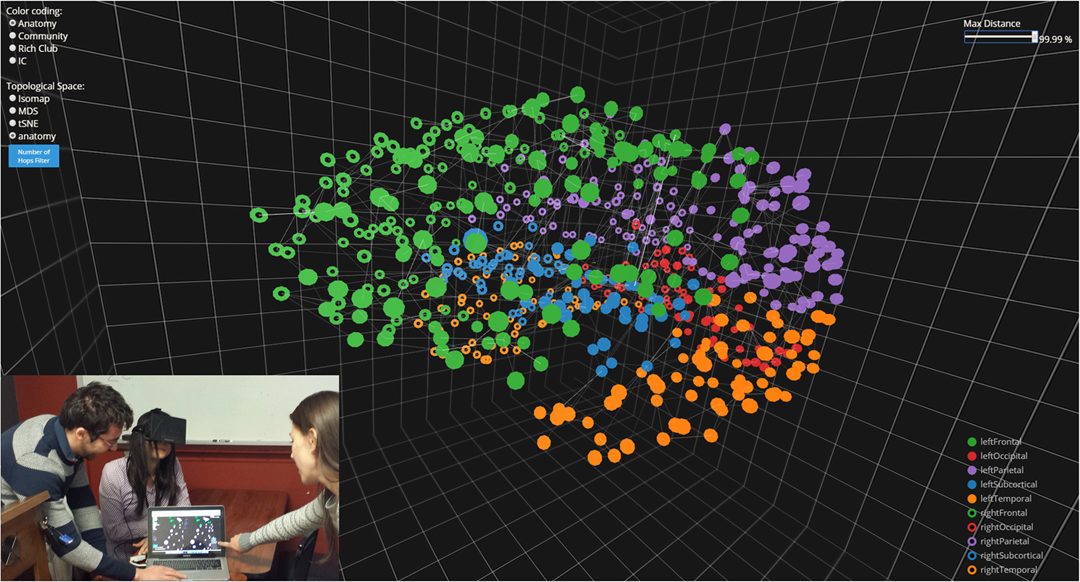
This paper describes novel methods for constructing the intrinsic geometry of the human brain connectome using dimensionality-reduction techniques. We posit that the high-dimensional, complex geometry that represents this intrinsic topology can be mathematically embedded into lower dimensions using coupling patterns encoded in the corresponding brain connectivity graphs.
We tested both linear and nonlinear dimensionality-reduction techniques using the diffusion-weighted structural connectome data acquired from a sample of healthy subjects. Results supported the nonlinearity of brain connectivity data, as linear reduction techniques such as the multidimensional scaling yielded inferior lower-dimensional embeddings. To further validate our results, we
demonstrated that for tractography-derived structural connectome more influential regions such as rich-club members of the brain are more centrally mapped or embedded. Further, abnormal brain connectivity can be visually understood by inspecting the altered geometry of these three-dimensional (3D) embeddings that represent the topology of the human brain, as illustrated using simulated lesion studies of both targeted and random removal. Last, in order to visualize brain’s intrinsic topology we have developed software that is compatible with virtual reality technologies, thus allowing researchers to collaboratively and interactively explore and manipulate brain connectome data.
Keywords: Diffusion MRI, Tractography, Dimensionality reduction, Virtual reality, Connectomics
Resources
Citation
Ye, A. Q., Ajilore, O. A., Conte, G., GadElkarim, J., Thomas-Ramos, G., Zhan, L., Yang, S., Kumar, A., Magin, R. L., Forbes, A. G., Leow, A. D., The intrinsic geometry of the human brain connectome, Brain Informatics, pp. 197–210, October 22nd, 2015.